We know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.

The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls and are projected from ground with same speed at same angle with the horizontal. The ball and collide with the wall during their flight in air and all three collide perpendicularly with the wall as shown in figure.

The vertical component of velocity of balls wiht which they are projected is
Undeterminable
The correct Answer is:A
Vertical component
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions

A particle of mass 3m is projected from point-A with speed 3v0 as shown in figure. When the particle is at point P, it explodes in three identical particles choose the INCORRECT statement regarding the physical quantities just before and just after explosion
View SolutionA particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View SolutionThe potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs x will be
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionConsider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is :
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.
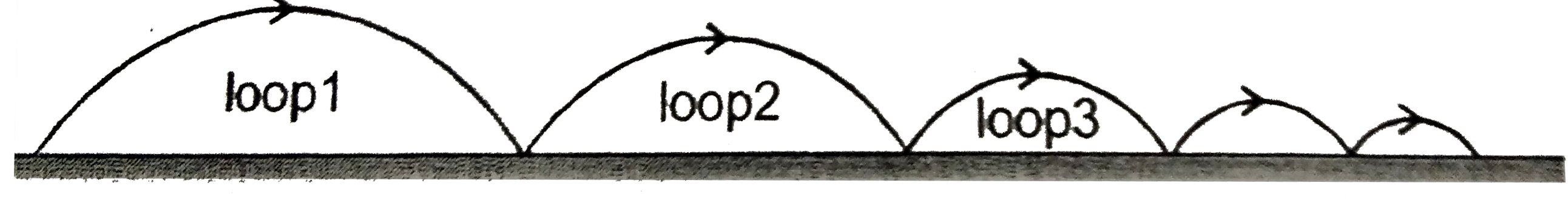
Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The ratio of maximum height reached by ball in first loop and second loop (H1H2) is :
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth & (ii) the collision is elastic If both the considered then the path of ball is as follows. Now if collision is inelastic and surface is rough then the path is as follows. Successive range is decreasing . Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change. Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30^(@) with horizontal and it is known that after collision with the floor its speed becomes (u)/(sqrt(3)) . Then answer the following questions. If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :
View SolutionWe know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.

The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls A,B, and C are projected from ground with same speed at same angle with the horizontal. The ball A,B and C collide with the wall during their flilght in air and all three collide perpendicularly with the wall as shown in figure.

If the total time taken by the ball A to fall back on ground is 4 seconds and that by ball B is 2 secons. Then, the maximum height attained by ball B from ground will be
View SolutionA billiard ball collides elastically with an identical stationary ball. The collision is not head on. Show that the directions of motion of the two balls are at right angles after the collision. Solve the problem in centre of mass frame as well as in lab frame.
View SolutionDerive velocities after the collision in terms of velocities before collision in elastic collision in one dimension case.
View SolutionObtain the expression for the velocities of the two bodies after collision in the case of one dimensional elastic collision ond discuss the specical cases.
View SolutionA ball rebounds after colliding with the floor, then in case of inelastic collision-
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA ball moving with speed u collides with an identical ball at rest. The velocities of two balls after collision are (If the collision is elastic):
View Solution
