We know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.

The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls $A, B,$ and $C$ are projected from ground with same speed at same angle with the horizontal. The ball $A, B$ and $C$ collide with the wall during their flilght in air and all three collide perpendicularly with the wall as shown in figure.

If the total time taken by the ball $A$ to fall back on ground is 4 seconds and that by ball $B$ is 2 secons. Then, the maximum height attained by ball $B$ from ground will be

$15 m$

$5 m$

$3 m$

$25 m$

Text Solution

Verified by Experts

The correct Answer is:A

Time of flight of $A$ is 4 seconds which is same as the time of flight if wall was not there.
Time taken by $B$ to touch the inclined roof is 1 second.
Hence, $S = 20 t - \frac{1}{2} {gt}^{2} = 20 \times 1 - 5 \times 1^{2} = 15 m$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
We know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.

The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls $A, B,$ and $C$ are projected from ground with same speed at same angle with the horizontal. The ball $A, B$ and $C$ collide with the wall during their flight in air and all three collide perpendicularly with the wall as shown in figure.

The vertical component of velocity of balls wiht which they are projected is
A $20 m / s$
B $10 m / s$
C $10 \sqrt{3} m / s$
DUndeterminable
Question 2 - Select One
In case of elastic collision,at the time of impact
ATotal K.E of colliding bodies is conserved
Btotal K.E. of colliding bodies is conserved
Ctotal K.E. of colliding bodies decreases
Dtotal momentum of colliding bodies decreases
Question 3 - Select One
Consider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is

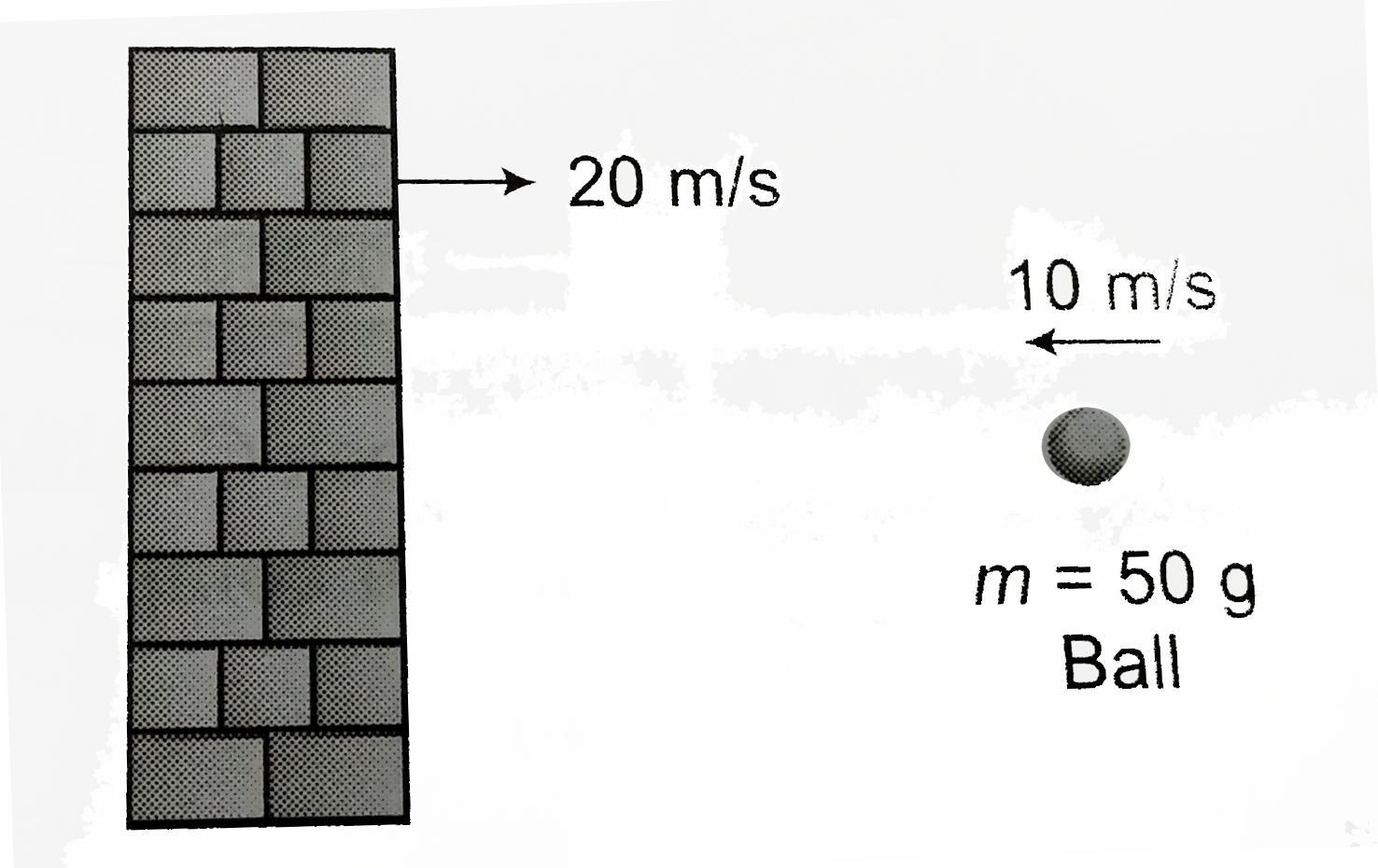A $30 J$
B $60 J$
C $90 J$
D $120 J$