If α is the root of the equation x−tanx=3 where αε(π2,3π2), then which of the following is/are correct? (where [.] denotes the greatest integer function and {.} fractional part function)
limx→α+[max(tanx,{x})x−3]=1
limx→α+[mi(tanx,{x})x−3]=1
limx→α−[min(tanx,{x})x−3]=0
limx→α−[max(tanx,{x})tannx]=1
The correct Answer is:A, B, C, D
Shown in the figure
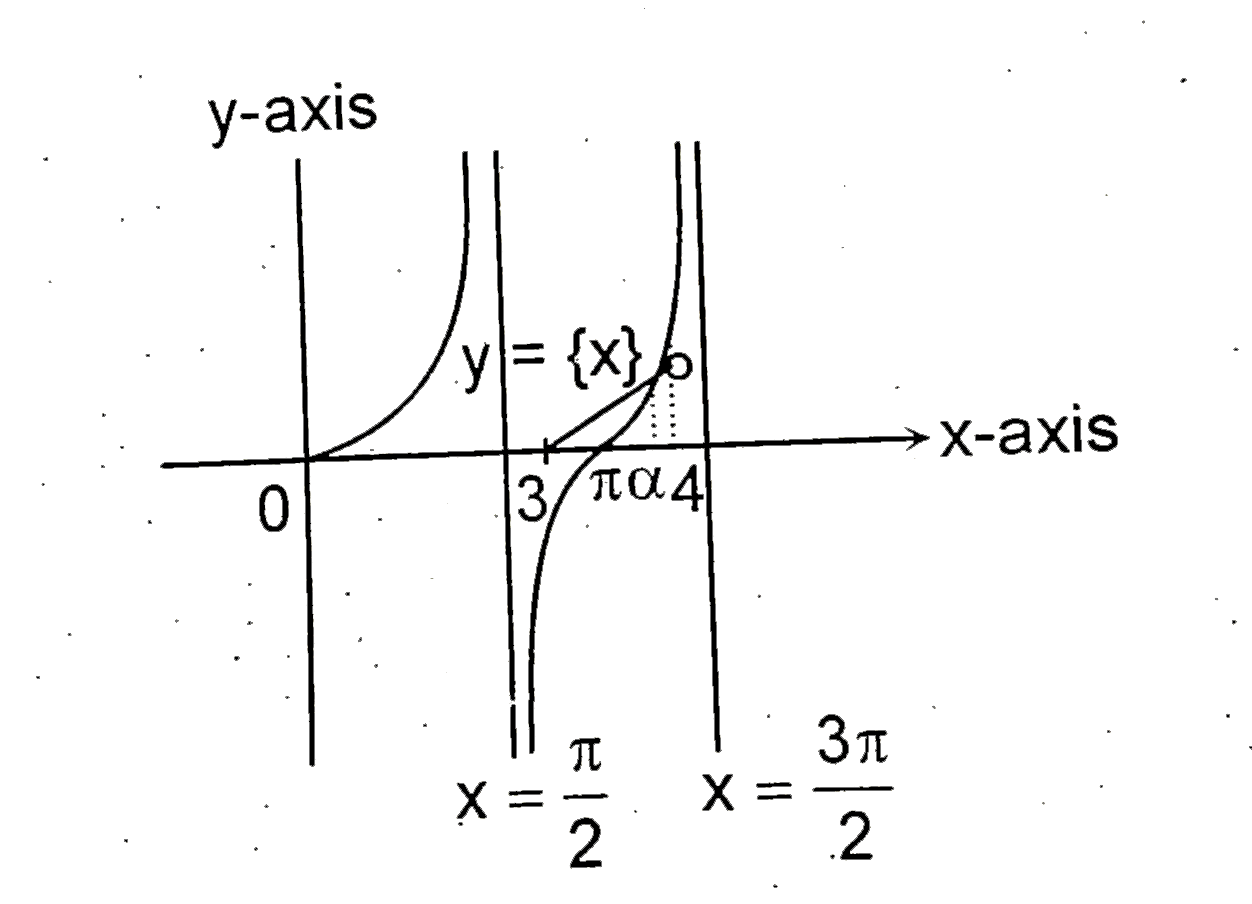
Topper's Solved these Questions
Similar Questions
If α is the root of the equation x−tanx=3 where α∈(π2,3π2): then which of the following is/are ecorrect ?, (where [.] denotes the greatest integer function and () fractional part function)
View Solution∫50[x]{x}dx (where [.]denotes greatest integer function and{.} denotes fractional part of function is
View Solution
Knowledge Check
- Question 1 - Select One or More
Which of the following is/are unity? (where [.] and {.} denote the greatest integer and fractional part functions, respectively)
Alimx→∞sin(x2+2x2+1)Blimx→0[x2+2x2+1]Climx→∞{x2+2x2+1}Dlimx→∞(x2x2+1) - Question 2 - Select One
The function f(x)={x}sin(π[x]), where [.] denotes the greatest integer function and {.} is the fractional part function, is discontinuous at
Aall xBall integer pointsCno xDx which is not an integer
Solve the following inequalities (where [*] denotes greatest integer function and {*} represent fractional part function) [2x2−x]<1
View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
View SolutionSolve the following equations
x2−3−{x}=0
where [x] denotes the greatest integer and {x} fractional part.View SolutionThe sum of solutions of the equation 2[x]+x=6{x} is (where [.] denotes the greatest integer function and {.} denotes fractional part function)
View SolutionConsider the function f(x) = {x+2} [cos 2x] (where [.] denotes greatest integer function & {.} denotes fractional part function.)
View SolutionFind x if 4x,5[x],6{x} are sides of a triangle ( where [ .] denotes the greatest integers function and {.} denotes fractional part function)
View Solution

