If ∀h∈R−{0}, two distinct tangents can be drawn from the points (2+h,3h−1) to the curve y=x3−6x2−a+bx then ab is equal to _____
Text Solution
The correct Answer is:1
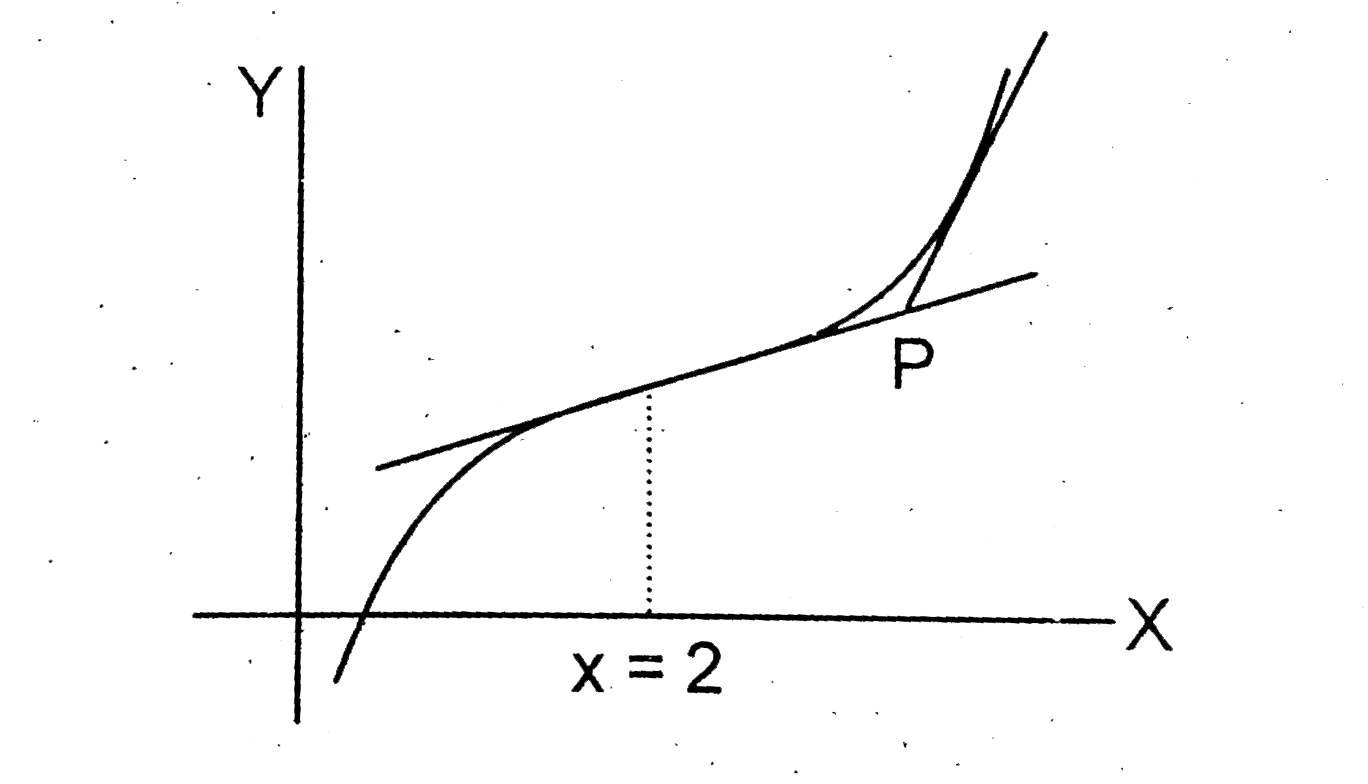
y''=0⇒x=2
Let P be the point of inflection
So P≡(2,2b−a−16)
Equation of tangent line passing through inflection
Point: y=(b−12)x−a+8…….(1)
Let Q≡(2+h,3h−1)
Locus of Q:3x−y=7…….(2)
From equation (1) and (2) we get !
So, a=15 adn b=15
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2rhy=0The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2hy=0The number of real tangents that can be drawn from (2, 2) to the circle x2+y2−6x−4y+3=0, is
A0B1C2D3
Let two distinct tangents that are drawn from a point (p,p+1) on the line y=x+1 to the curve y=2x2. Also k is the least positive integral value of p .The value of k is
View SolutionThe slope of the tangent at the point (h,2h) on the circle x2+y2=5 where (h>0) is
View SolutionThe slope of the tangent at the point (h, 2h) on the circle x2+y2=5 is (where h>0)
View SolutionThe equations of the tangents drawn from the origin to the circle x2+y2+2rx+2hy+h2=0, are :
View SolutionThe distance betwcen the point (1, 1) and the tangent to the curve y= e2x+x2 drawn from the point x =0 is
View Solution
