Let $y = f (x)$ be the solution of the differential equation $\frac{d y}{d x} + \frac{k}{7} x tan x = 1 + x tan x - sin x,$ where $f (0) = 1$ and let $k$ be the minimum value of $g (x)$ where $g (x) = max ∣ ∣ ∣ \frac{\sqrt{193} - 1}{2} cos y + cos (y + \frac{π}{3}) - x ∣ ∣ ∣$ where $y ε R$ then
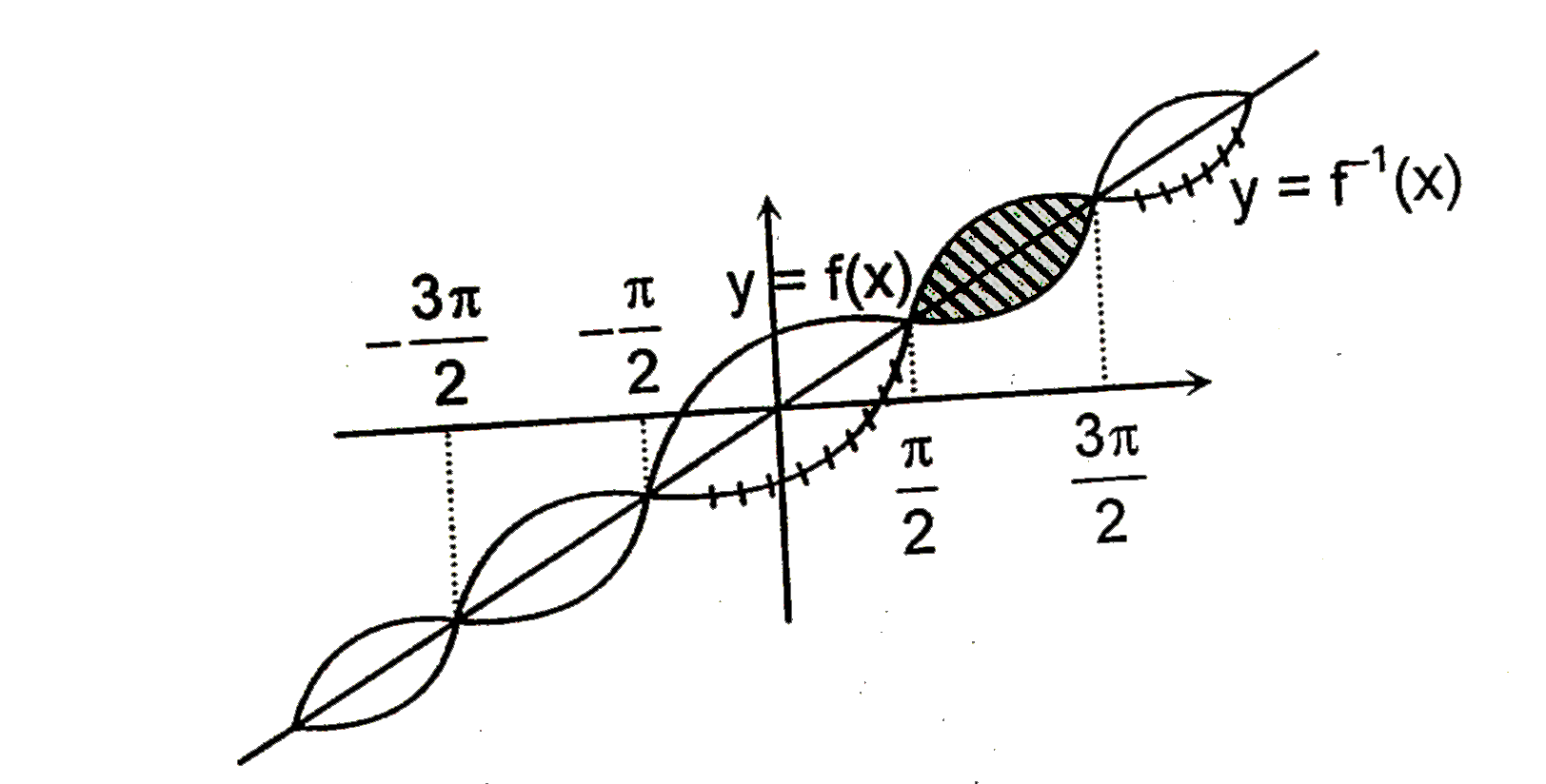
Area bounded by $y = f (x)$ and its inverse between $x = \frac{π}{2}$ and $x = \frac{7 π}{2}$ is

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Let $y = f (x)$ be the solution of the differential equation $\frac{d y}{d x} + \frac{k}{7} x tan x = 1 + x tan x - sin x,$ where $f (0) = 1$ and let $k$ be the minimum value of $g (x)$ where $g (x) = max ∣ ∣ ∣ \frac{\sqrt{193} - 1}{2} cos y + cos (y + \frac{π}{3}) - x ∣ ∣ ∣$ where $y ε R$ then
Number of solution of the equation $f (x) = 2^{x} - x^{2} + x + cos x$ is equal to
A3
B1
C2
D4
Let y=y(x) be the solutio of the differential equation $\frac{d y}{d x} + 2 y = f (x)$ , where $f (x) = {\begin{matrix} 1 & x \in [0, 1] 0 & otherwise \end{matrix}$ . If y(0)=0, then $y (\frac{3}{2})$ is
A $\frac{e^{2} - 1}{2 e^{3}}$
B $\frac{e^{2} - 1}{e^{3}}$
C $\frac{e^{2} + 1}{2 e^{4}}$
D $\frac{1}{2 e}$
The solution of the differential equation $2 x^{2} y \frac{dy}{dx} = tan (x^{2} y^{2}) - 2 x y^{2}$ , where $y = \sqrt{\frac{π}{2}}$ where x =1, is
A $sin (x^{2} y^{2}) = e^{x - 1}$
B $sin (x^{2} y^{2}) = x$
C $cos (x^{2} y^{2}) + x = 0$
D $sin (x^{2} y^{2}) = e . e^{x}$