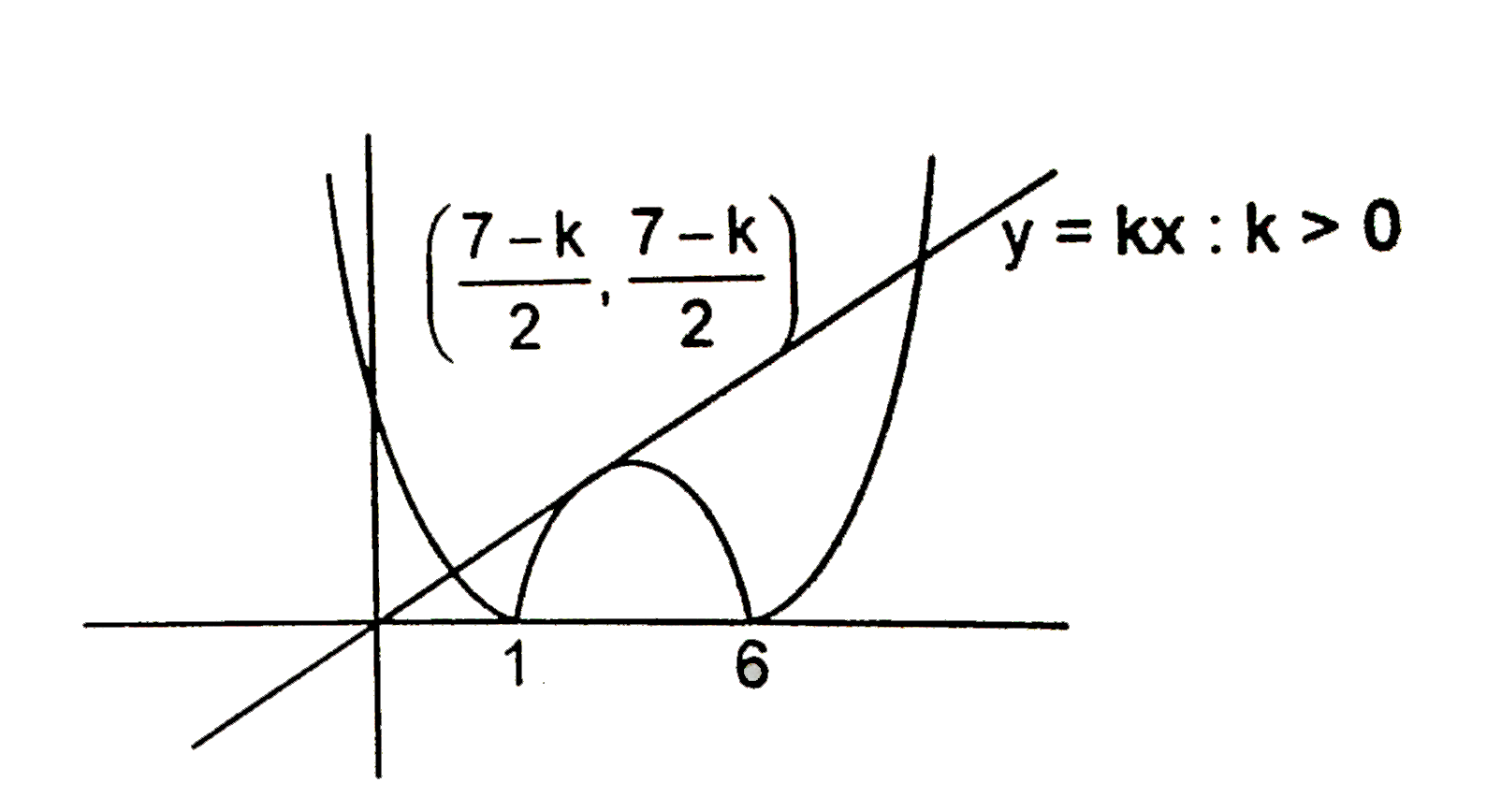
The complete set of non-zero values of $' k'$ such that the equation $∣ ∣ x^{2} - 7 x + 6 ∣ ∣ = k x$ is satisfies by at least one and at most three real value(s) of $x$ is $(- \infty, l_{1}], \cup [l_{2}, \infty)$ then $\frac{| l_{1} - l_{2} |}{2}$ is equal to __________.

Text Solution

Verified by Experts

The correct Answer is:7

So, $- 2 x + 7 = k$
$\Rightarrow x = \frac{7 - k}{2}$
Also $- \frac{{(7 - k)}^{2}}{4} + 7 (\frac{7 - k}{2}) - 6 = k (\frac{7 - k}{2})$
$\Rightarrow k = 7 + \sqrt{24}, 7 - \sqrt{24}$ (Rejected)
So: $k \in [7 - \sqrt{24, \infty})$
Similarly consier case -II i $k < 0$ then $k ε (- \infty, - (7 + \sqrt{24})]$

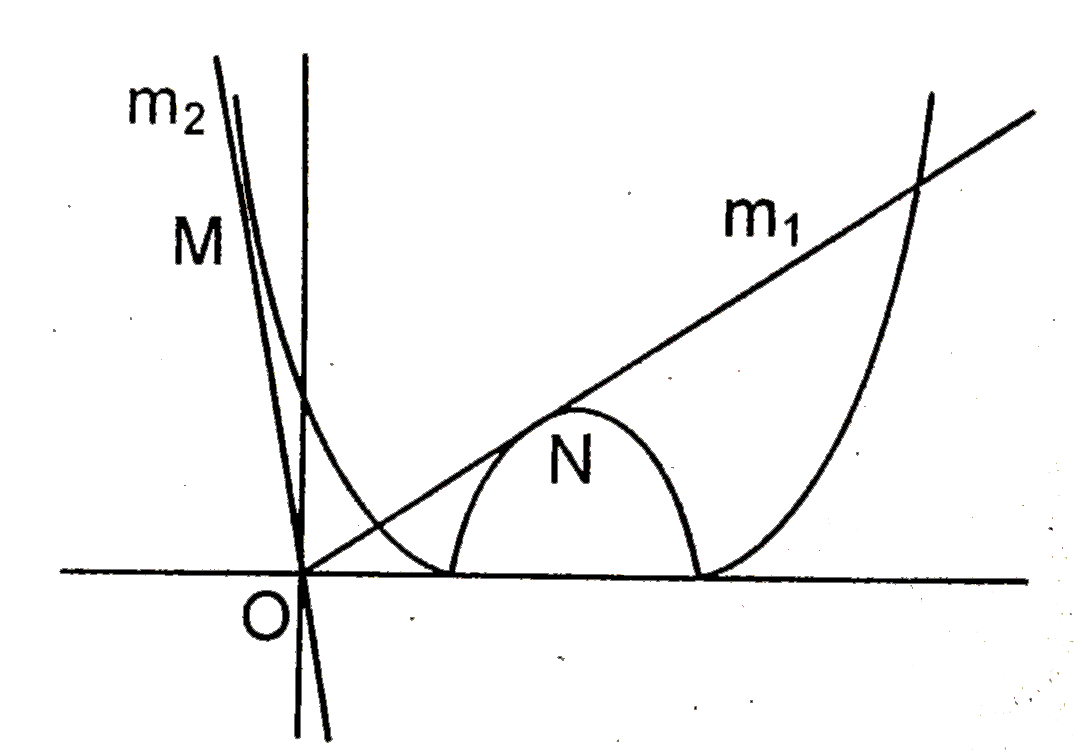
Second Method
Clealy : $m_{1} < k < k_{2}$
For slope of $O N$
$(x^{2} - 7 x = 6) = k x$
Must have equal roots
For slope of OM
$x^{2} - 7 x + 6 = k x$
Must have equal roots

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the figure above, if $l_{1} ∣ ∣ l_{2}$ , what is the value of x?
A $90$
B $85$
C $75$
D70

FIITJEE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile