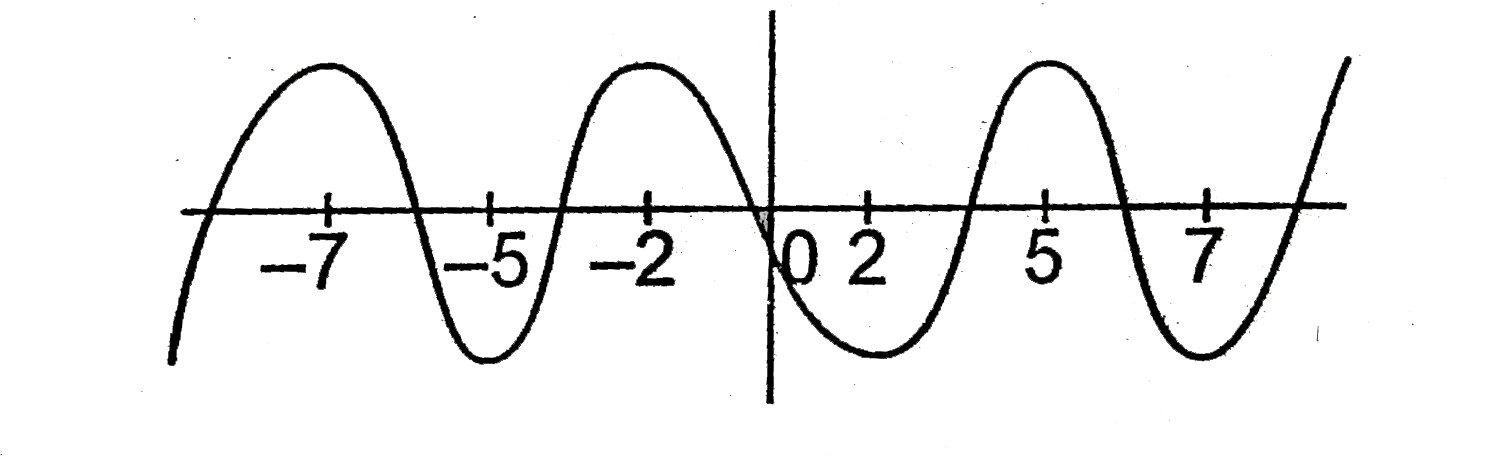
Let f(x)=ax17+bsinx.sin2x.sin3x+cx2sgn(sinx)+dlog(x+√1+x2)+x(|x+1|−|x−1|)(ex−e−xex+e−x) be defined on te set of real numbers, (a>0,b,c,d∈R) if f(−7),f(−5)=−5,f(−2)=3, then the minimum number of zeroes of the equation f(x)=0 is equal to ________.
The correct Answer is:7
f is an odd function
So, f(7)=−7,f(5)=f(2)=3
x→−∞,f(x)→∞
x→∞,f(x)→∞
Topper's Solved these Questions
Similar Questions
Knowledge Check
If f(x) = sin x then ∫ef(x)(xcos3x−f(x))1−(f(x))2dx is equal to
Aef(x)(x−sinx)+CBef(x)(x−secx)+CCef(x)(x+secx)+CDef(x)(x+sec2)+C
If f(x)=sin−1x√1−x2,then(1−x2)fx−xy(x)= 1 (b) −1 (c) 0 (d) none of these
View SolutionIf f(x) is a twice differentiable function such that f(a)=0, f(b)=2, f(c)=-1,f(d)=2, f(e)=0 where a < b < c < d e, then the minimum number of zeroes of g(x)=f'(x)2+f''(x)f(x) in the interval [a, e] is
View SolutionIf f(x) is a twice differentiable function such that f(a)=0, f(b)=2, f(c)=-1,f(d)=2, f(e)=0 where a < b < c < d e, then the minimum number of zeroes of g(x)=f'(x)2+f''(x)f(x) in the interval [a, e] is
View SolutionIf f(x)=sin(log)e{√4−x21−x} , then the domain of f(x) is _____ and its range is __________.
View SolutionIf f(x)=sin(log)e{√4−x21−x} , then the domain of f(x) is _____ and its range is __________.
View SolutionLet f:R→R be defined as f(x)=7esin2x–ecos2x+2, then the value of √7fmin+fmax is equal to
View SolutionLet F(x)=(sinx−12)(lnx−1)4(x−2)3(tanx−√3)5(ex−e2)(x−3)6(sin2x−1) solve the following inequalities for x∈(0,2π)
View Solution
