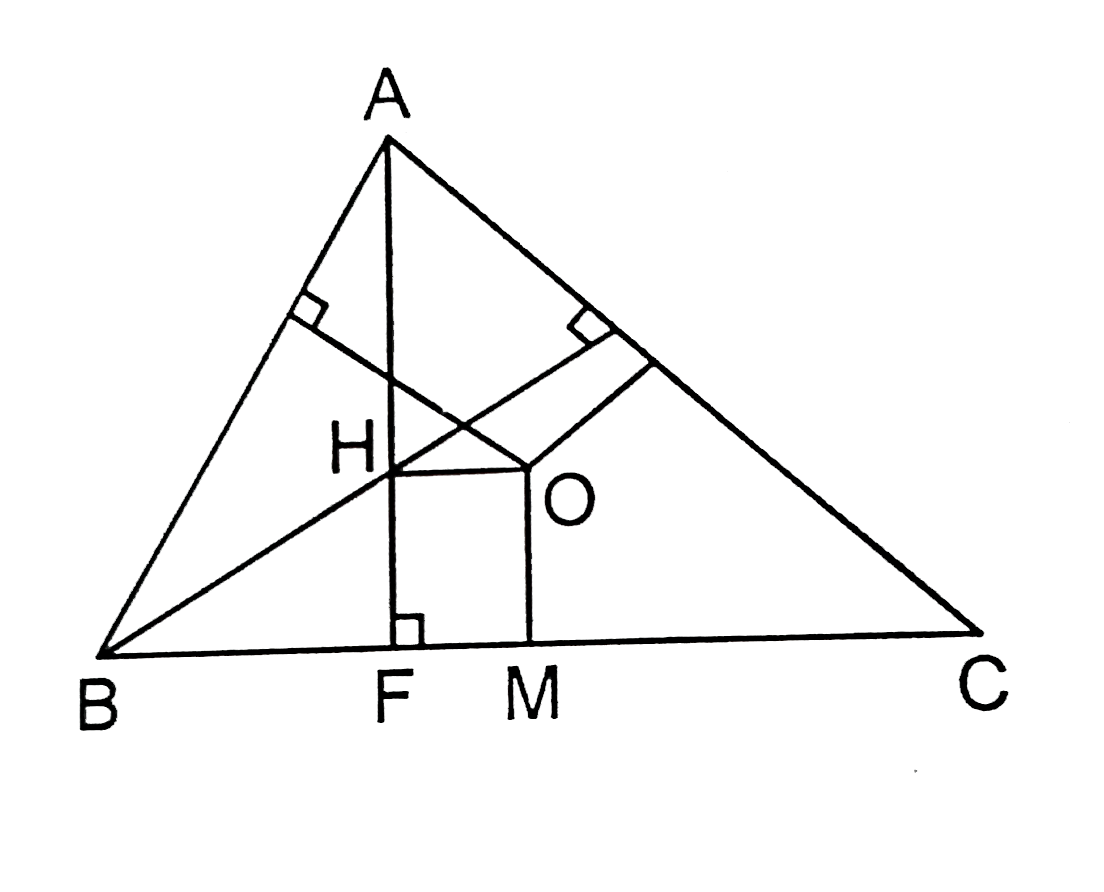
A rectangle HOMF has sides HO=11 and OM=5. A triangle ABC has H as the intersection of the altitude, O the centre of the circumscribed circle M the mid point of BC, and F the foot of the altitude from A, then
A
perimeter of ΔABCis greater than 70
B
area of ΔABC in integer
C
one side of ΔABC in rational
D
all sides of ΔABCare lessthan 30
Text Solution
The correct Answer is:A, B, C, D
Centroid G of triangle is collinear with H and O and G lies two third of way from A to M, therefore H is two third of the way from A to F. So AF=3×OM=15
Since ∠HFB=∠AFC,∠HBF=∠ACF
So ,ΔBFH and ΔAFC are similar
BFHF=AFFC⇒BF.FC=FA.HF=75
Now BC2=(BF+CF)2=(BF−CF)2+4BF.FC
But FC−BF=(FM+MC)−(BM−FM)=2FM=22
BC=√222+4×75=28
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If in a !ABC , the altitudes from the vertices A , B , C on the opposite sides are in H.P., then sin A, sin B , sin C are in
AA.P.BG.P.CH.P.DNoneIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CFΔABCis a equilateral triangle. O is the point of intcrscction of al titudes AL,BMandCN. If OA=16cm, what is the semi-perimeter (in cm) of the triangle ABC?
A8√3B12√3C16√3D24√3
If in a triangle ABC, the altitude AM be the bisector of ∠BAD, where D is the mid point of side BC, then prove that (b2−c2)=a22.
View SolutionΔABC is an acute angled triangle. CD be the altitude through C. If AB=8,CD=6 , then the distance between the mid-points of AD and BC is
View SolutionIf in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P, then sin A, sin B, sin C are in
View SolutionIf the mid points of the sides AB and AC of a triangle ABC are (3, 5), (-3,-3) then the length of the side BC is
View SolutionIn ΔABC,A(5,6) and its centroid is (2,3) then mid point of the side BC is
View Solution
