A particle $P$ moves on the line $y = x, x \leq 0$ with constant speed $u m / sec$ . Another particle $Q$ revolves along the circke ${(x - 1)}^{2} + y^{2} = \frac{1}{9}$ with constant speed $\frac{ω}{3} m / sec$ . In anticlockwise directio, let at $t = 0$ , both $P$ and $Q$ simultaeously started, $P$ from the point $(0, 0)$ and $Q$ from he point $(\frac{2}{3}, 0)$ . Further at any time instant $t$ sec, let the distance of theri separation is $r (t) m$ . Also it was observed that at time $t_{0}$ sec, both $P$ and $Q$ are at their closest distance of approach, denoted by $r_{minimum} m$ , then choose the correct statements from among the following

A

$[12 r_{minimum}] = 4$ (where [.] denotes the greatest integer function)

B

$t_{0} = \frac{7 π}{4 ω}$ sec

C

$t_{0} = \frac{π}{2 ω}$ sec

D

$2 r (t) \frac{d r (t)}{d t} ∣_{t = \frac{7 π}{2 ω} sec} = \frac{16 ω}{3 π} m^{2} / sec$

Text Solution

Verified by Experts

The correct Answer is:A, B

Eg. of common normal $y - 0 = - 1 (x - 1)$
$y = - x + 1, {(x - 1)}^{2} + y^{2} = \frac{1}{3}$
$x + y - 1 = 0, 2 y^{2} = \frac{1}{9}$
$x - 1 = y, y^{2} = \frac{1}{3 \sqrt{2}}$

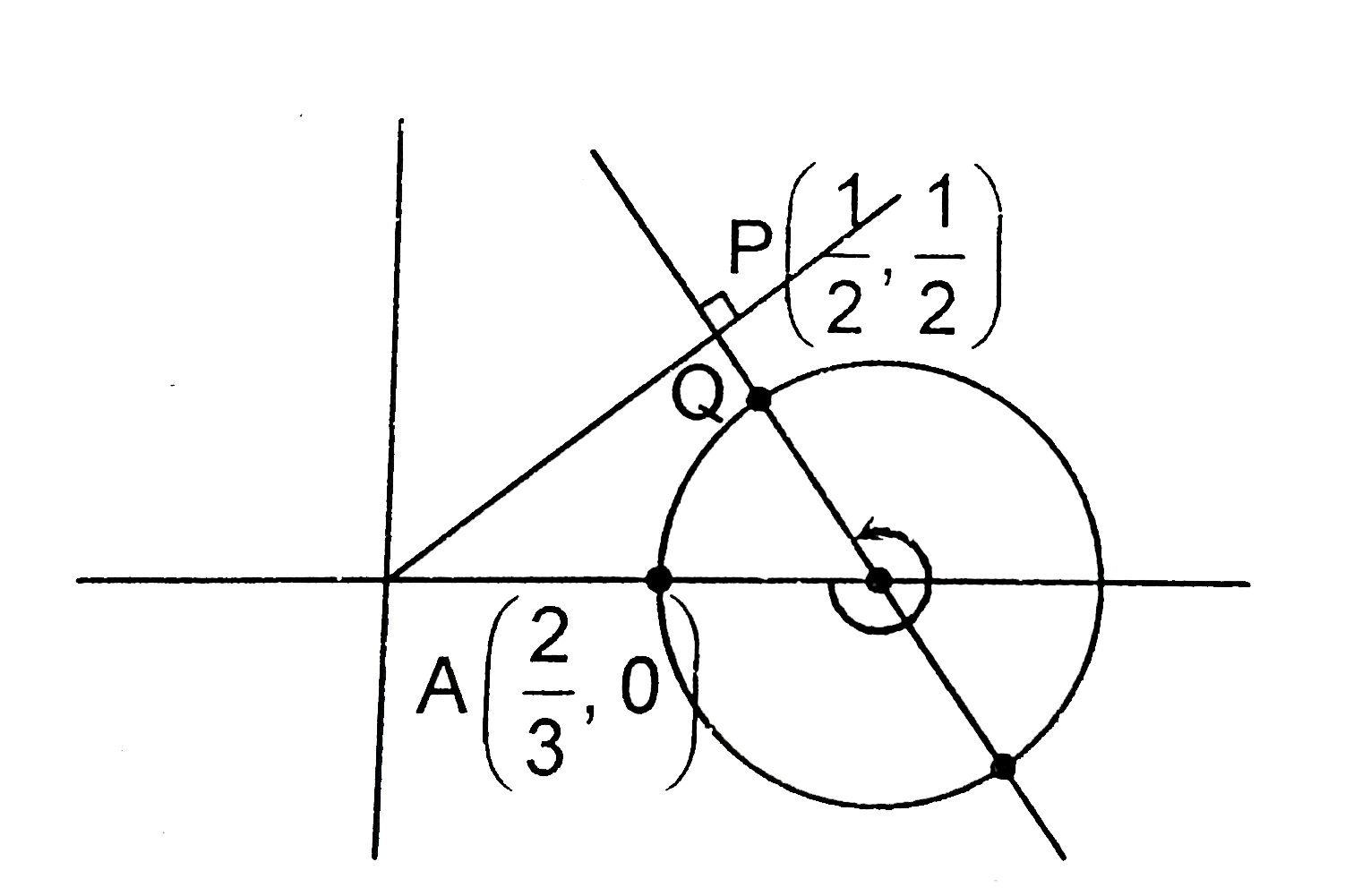
Clearly shortest distance of approach is along common normal whose equation is $x + y = 1 = 0$ .
So, when they are at their closest distance $P$ must be at $(\frac{1}{2}, \frac{1}{2})$ and $Q$ must be at $(1 - \frac{1}{3 \sqrt{2}}, \frac{1}{3 \sqrt{2}})$ covering angle $\frac{7 π}{4}$ on the circle .
Since $P$ and $Q$ happened to be at these points at same time so we have $t_{0} = \frac{7 π}{4 w} = \frac{1}{\sqrt{2 u}}$ also at this instance
$t_{0}, r_{min} = \frac{3 - \sqrt{2}}{3 \sqrt{2}} \Rightarrow [12 r_{min}] = [6 \sqrt{2} - 4] = 4$
Also at any time instant $t_{1}$ co-ordinate of $P, Q$ are $(\frac{u t}{\sqrt{2}}, \frac{u t}{\sqrt{2}})$ at $Q (1 + \frac{cos (ω t)}{3}, + sin (\frac{ω t}{3}))$
$∴ r^{2} (t) = {(\frac{u t}{\sqrt{2}} - 1 - \frac{cos (ω t)}{3})}^{2} + {(\frac{u t}{\sqrt{2}} - \frac{sin (ω t)}{3})}^{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Particle $A$ moves with $4 m / s$ along positive $y -$ axis and particle $B$ in a circle $x^{2} + y^{2} = 4$ (anticlockwise) with constant angular velocity $ω = 2 r a d / s$ . At time $t = 0$ particle is at $(2 m, 0)$ . Then
Amagnitude of relative velocity between them at time $t$ is $8 sin t$
Bmagnitude of relative velocity between them is maximum at $t = \frac{π}{4} s$
Cmagnitude of relative velocity between them is maximum at $t = \frac{π}{2} s$
Dmagnitude of relative velocity between them at time $t$ is $8 sin 2 t$
Question 2 - Select One
Two particles each of mass m and charge q are separated by $r_{1}$ and the system is left free to move at t = 0. At t = 1, both the particles are found to be separated by $r_{2}$ . The speed of each particle is
A $\frac{q m}{4 π ε_{0} r_{1} r_{2}}$
B $\frac{q}{r_{1} r_{2} \sqrt{(r_{2}^{2} - r_{1}^{2}) / 4 π ε_{0} m}}$
C $\frac{\sqrt{2} q}{r_{1} r_{2} \sqrt{(r_{2}^{2} - r_{1}^{2}) / 4 π ε_{0} m}}$
D $q \sqrt{\frac{(r_{2} - r_{1})}{4 π ε_{0} m r_{1} r_{2}}}$
Question 3 - Select One
At t = 2 sec., a particles is at $(1, 0, 0,) .$ It moves towards $(4, 4, 12)$ with a constant speed of 65 m/s. The position of the paritcle is measured in metres and the time is sec. Assuming constant velocity, the position of the particle at t = 3 s is,
A $(13 ˆ i - 120 ˆ j + 40 ˆ k)$
B $(40 ˆ i + 31 ˆ j - 120 ˆ k)$
C $(13 ˆ i - 40 ˆ j + 12 ˆ k)$
D $(45 ˆ i + 60 ˆ j + 180 ˆ k)$

FIITJEE-TEST PAPERS-MATHEMATICS

Home
Ask Doubt
Profile