A non-conducting hollow cone has charge density σ A path ABP is cut and removed from the cone. The potential due to the remaining portion of the cone at point 'P' is

56σRε0
524σRε0
53σRε0
512σRε0
The correct Answer is:D
Potential due to circular non conducting disc, Vc=σr2ε0 (where r is radius of disc)
So vP=(θ2π)(σ.l2ε0)
=(σl2ε0)(53πR(l))(12π=5σR12ε0

Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
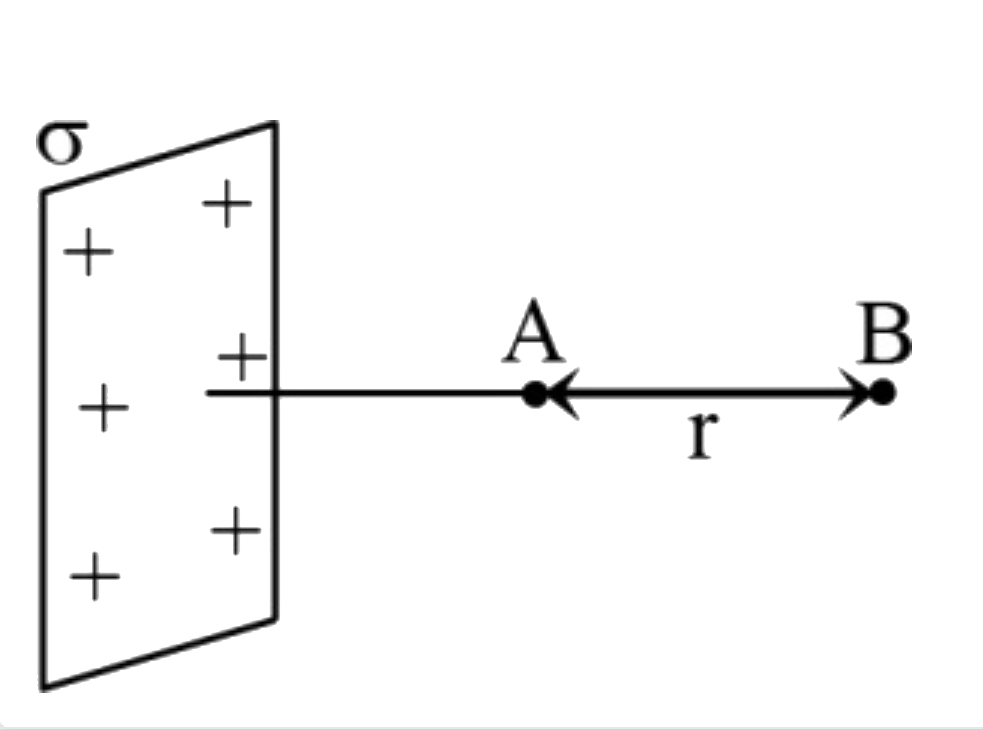
An infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
 View Solution
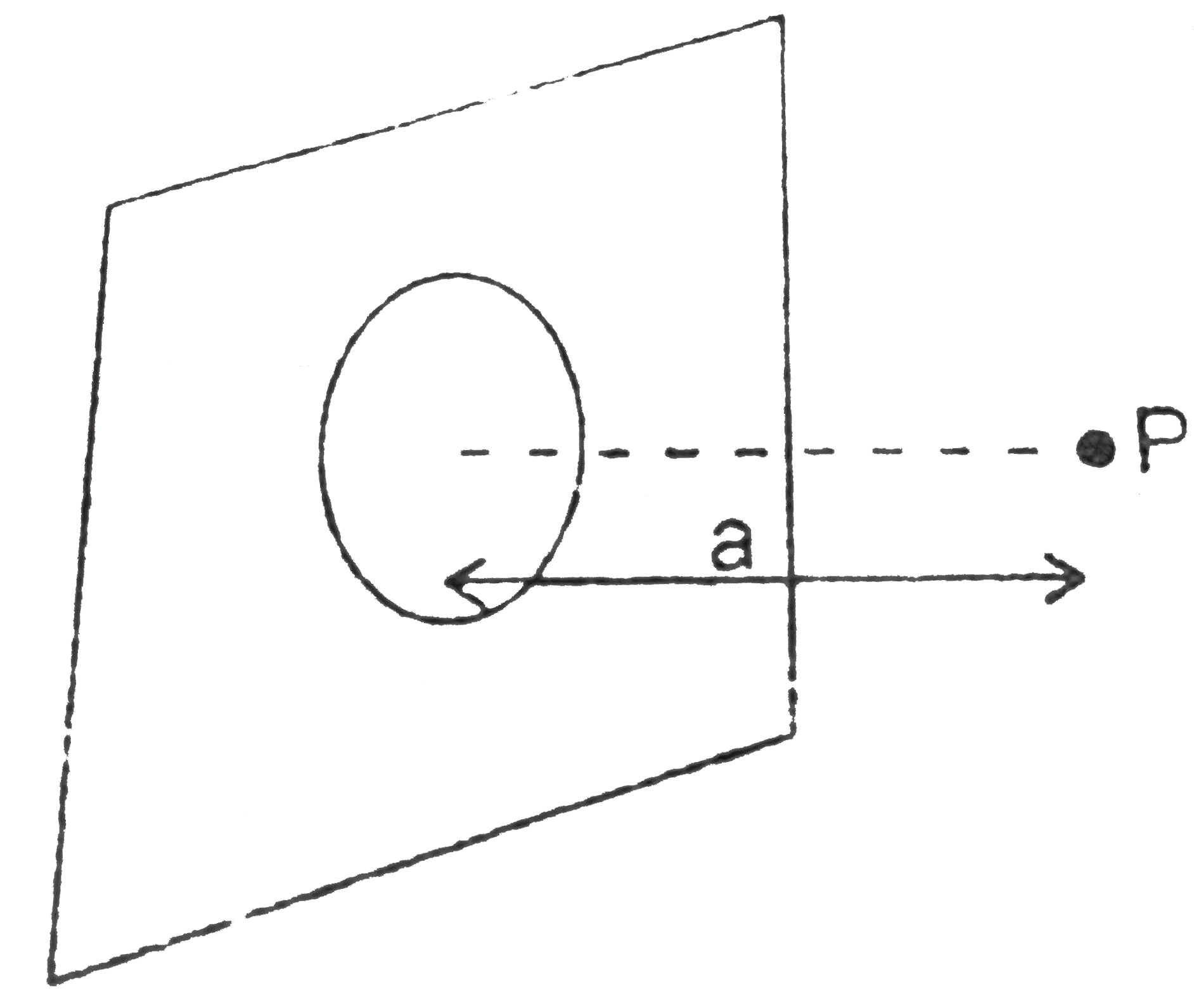
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
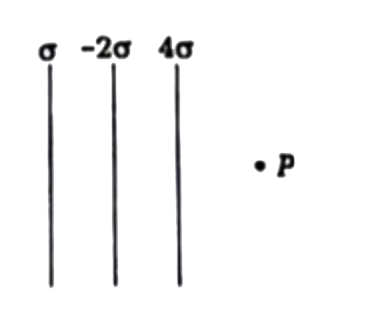 Aσε0Bσ2ε0C3σ2ε0D3σε0
Aσε0Bσ2ε0C3σ2ε0D3σε0 - Question 2 - Select One
A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
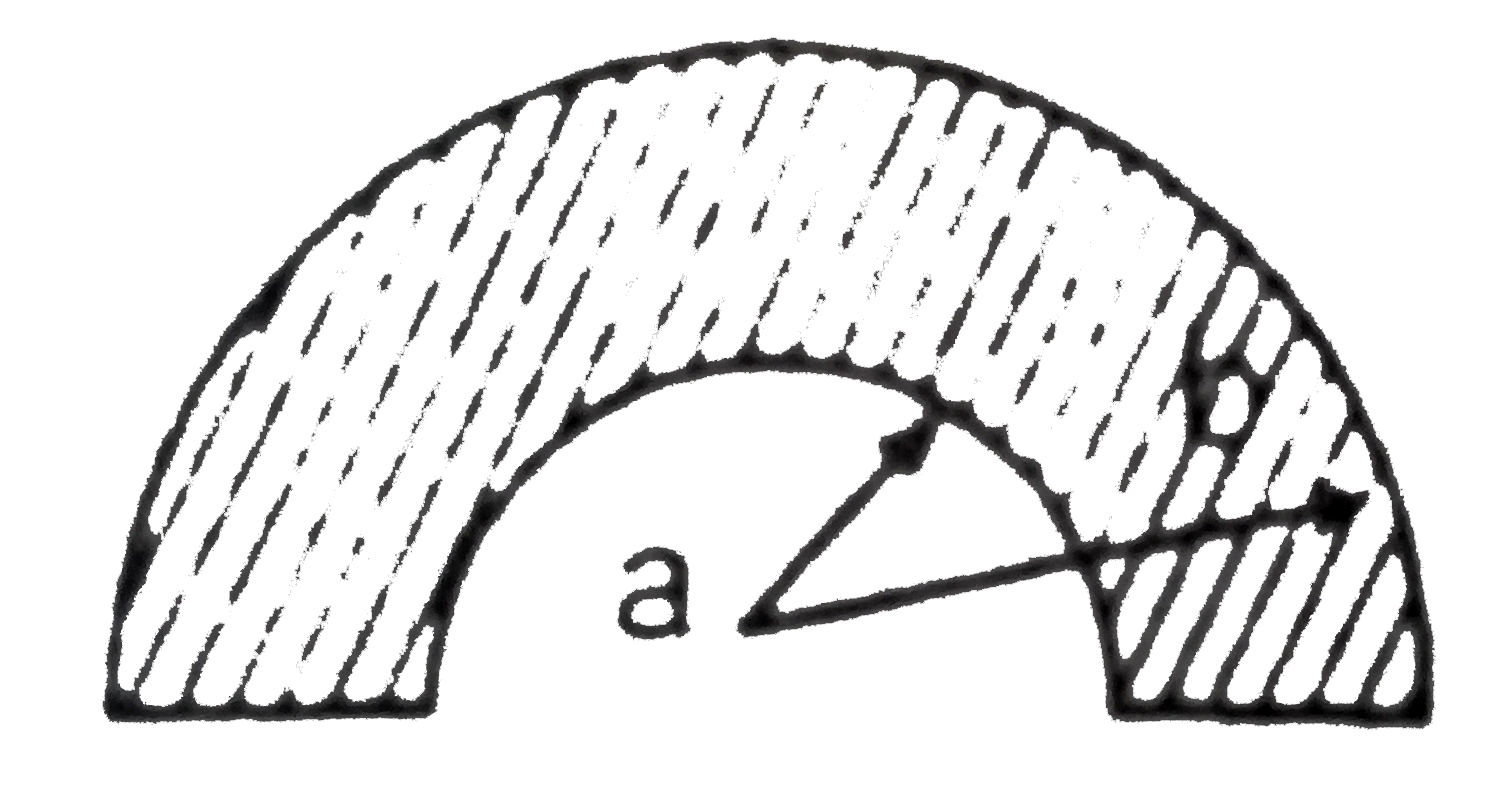 A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
A uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View SolutionA conducting shell having no charge has radius R. A point charge Q is placed in front of it at a distance r0 from its centre. Find potential due to charge induced on the surface of the shell at a point P inside the shell. Distance of point P from point charge Q is r.
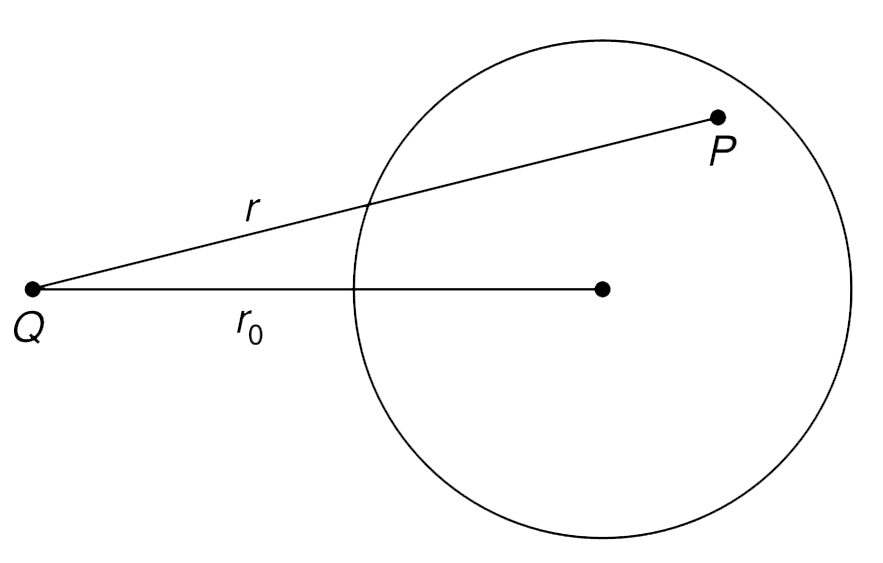 View Solution
View SolutionThere is an infinite non conducting sheet of charge having uniform charge density σ. The electric field at a point P at a distance x from the sheet is E0. Point O is the foot of the perpendicular drawn from point P on the sheet. A circular portio of radius r<<x centered at O is removed from the sheet. Now the field at point P becomes E0−ΔE. Find ΔE.
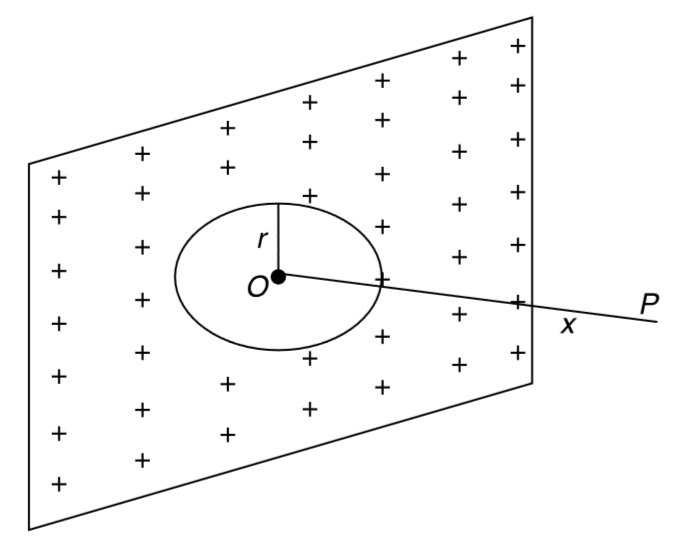 View Solution
View SolutionThe electric potential at surface of thin non-conducting sheet with charge density σ is V0. Show that the electric potential at a distance x from infinite sheet can be written as
V=V0−σ2∈0xView SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
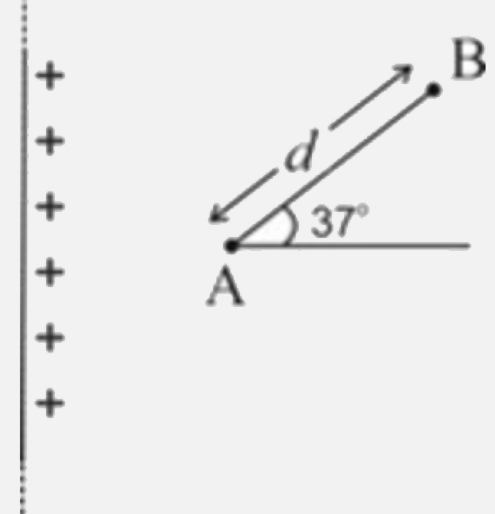 View Solution
View SolutionIn front of a uniformly charged infinite non-conducting sheet of surface charge density σ, a point charge q0 is shifted slowly from a distance a to b(b>a). If work done by external agent is W, then find out relation between the given parameters.
View Solution

