Magnetic field exist in the space and given as →B=−B0l2x2ˆk, where B0and l positive constants. A particle having positive charge 'q' and mass 'm' is pojected wit speed 'v0' along positive x axis from the origin. What is the maimum distance of the charged particle from the y-axis before it turns back due to the magnetic field. (Ignore any interaction other than magnetic field)
(ml2v03qB0)1/3
(3ml2v02qB0)1/3
(3ml2v0qB0)1/3
(ml2v0qB0)1/3
The correct Answer is:C
→F=q→v×→B
=q(vxˆi+vyˆj)→B
Fy=qB0l2x2vx
∫v00dvy=qB0ml2∫xmax0x2dx
v0=qB0ml2x2max3
xmax=(3ml2v0qB0)1/3
Alternate solution
Impulse momentum theorem along x -axis
∫xmax0qB0x2l2=vxdt=mv0
∴∫xmax0qB0x2l2=dx=mv0
∴xmax=(3ml2v0qB0)1/3
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
A positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
 View Solution
View SolutionElectric field E = – bx + a exists in a region parallel to the X direction (a and b are positive constants). A charge particle having charge q and mass m is released from the origin X = 0. Find the acceleration of the particle at the instant its speed becomes zero for the first time after release.
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
A−2mv0qB0Bmv0qBC−mv0qBD2mv0qB0 - Question 2 - Select One
A non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in the region of space between y=0 and y=d. A particle of mass m and positive charge q has velocity →v=3qB0dmˆi at origin O. Find the angle made by velocity of the particle withe the positive x-axis when it leaves the field. (Ignore any interaction other than magnetic field)
A90∘B30∘C60∘D45∘ - Question 3 - Select One
A particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
AZeroBmvqBC2mvqBDinfinity
A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
 View Solution
View SolutionA particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
View SolutionA positive charge q is projected in magnetic field of width mv√2qB with velocity v as shown in figure. Then time taken by charged particle to emerge from the magnetic field is
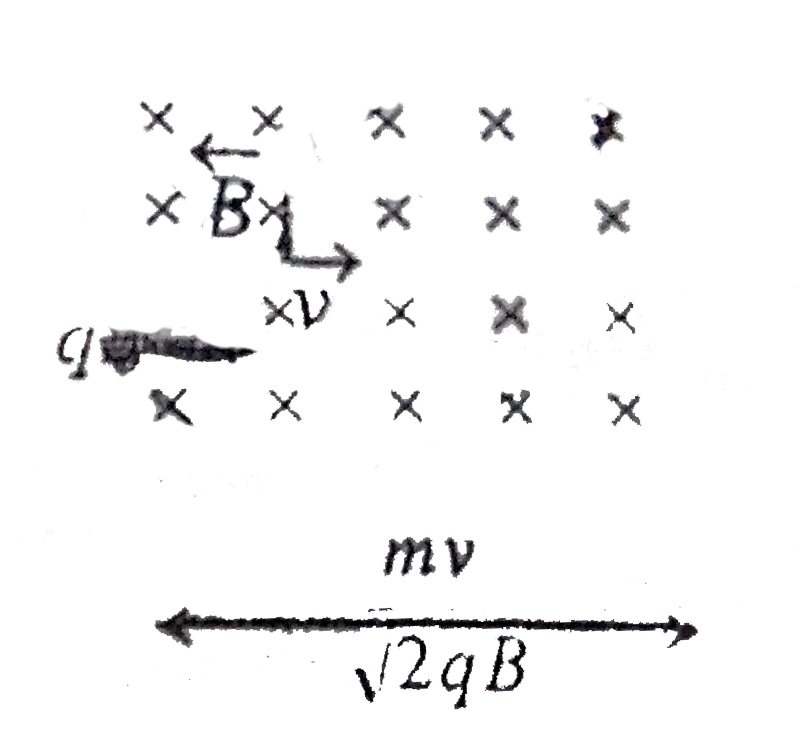 View Solution
View SolutionA uniform magnetic field B=B0ˆj exists in space. A particle of mass m and charge q is projected towards X-axis with speed v from a point (a,0, 0). The maximum value of v for which the particle does not hit the Y-Z plane is
View SolutionA magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
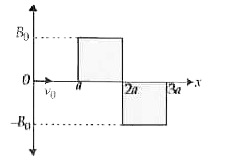
the magnetic field at x=a, The trajectory of the charge in this region can be like,View Solution

