A particle having charge and mass is projected with velocity from the origin in a region occupied by electric field and magnetic field such that and (take ). Find the time (in sec) when the magnitude of velocity of the charge particle becomes . (neglect the gravity)
The correct Answer is:8
sec
sec
So, sec
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
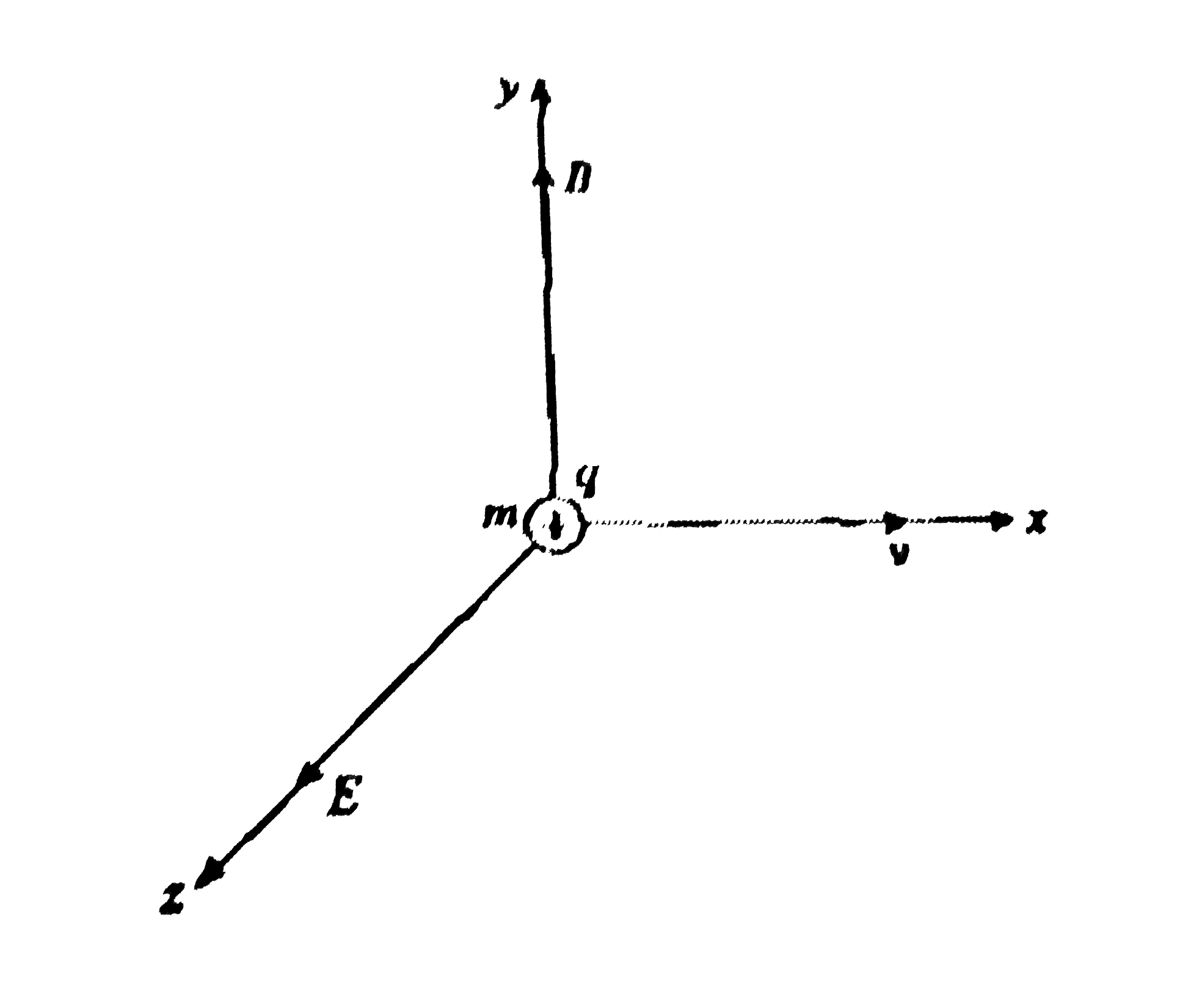
A particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are ginen by
B=+B0ˆj and →E=+E0ˆi.
Find the speed of the particle as a function of its X-coordinate.
View SolutionA charge particle of charge q, mass m is projected with a velocity →v=vˆi in a region of space where electric field strength →E=Eˆk and magnetic induction →B=Bˆj are present. The acceleration of the particle is:
View Solution
Knowledge Check
A particle of charge 'q' and mass 'm' is projected from the origin with velocity (u0ˆi+v0ˆj) in a gravity free region where uniform electric field −E0ˆi and uniform magnetic field −B0ˆi exist. Find the condition so that the particle would return to origin at least for once .
Aμ0B02πE0 is an integerB√u20+v20B0πE0 is an integerCv0B0πB0 is an integerDμ0B0πE0 is an integerA particle of charge q=4μC and mass m = 10 mg starts moving from the origin under the action of an electric field →E=4ˆi and magnetic field →B=(0.2T)ˆk. Its velocity at (x, 3, 0) is (4→i+3→j). The value of x is -
A11516mB12516mC13516mD14516m
A particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E=E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
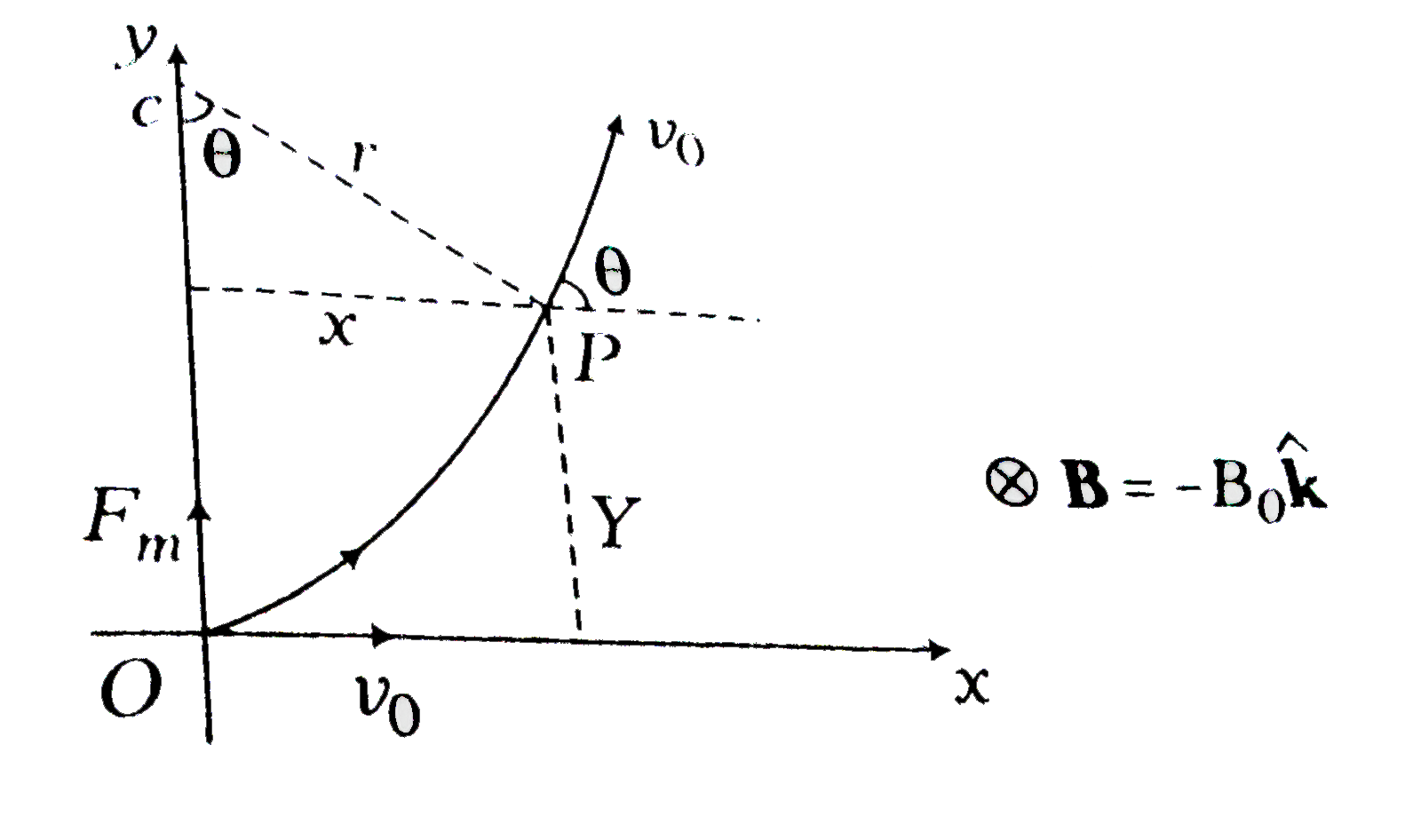
View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View Solution
