In the figure shown rod AB is light and rigid while rod CD is also rigid and hinged at midpoint O Rod can rotate without friction about O. The time period of small oscillation of rod CD is T=2π√mnk. Where m is mass of rod CD and k is spring constant of each spring. The value of n is

The correct Answer is:5
ml212α=−{2kθ2+kθ4}l2⇒α=−(5km)θ
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Find the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
 View Solution
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3g - Question 2 - Select One
In the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end. Rotational SHM of the rod (Mass m, length L) will occur only if-
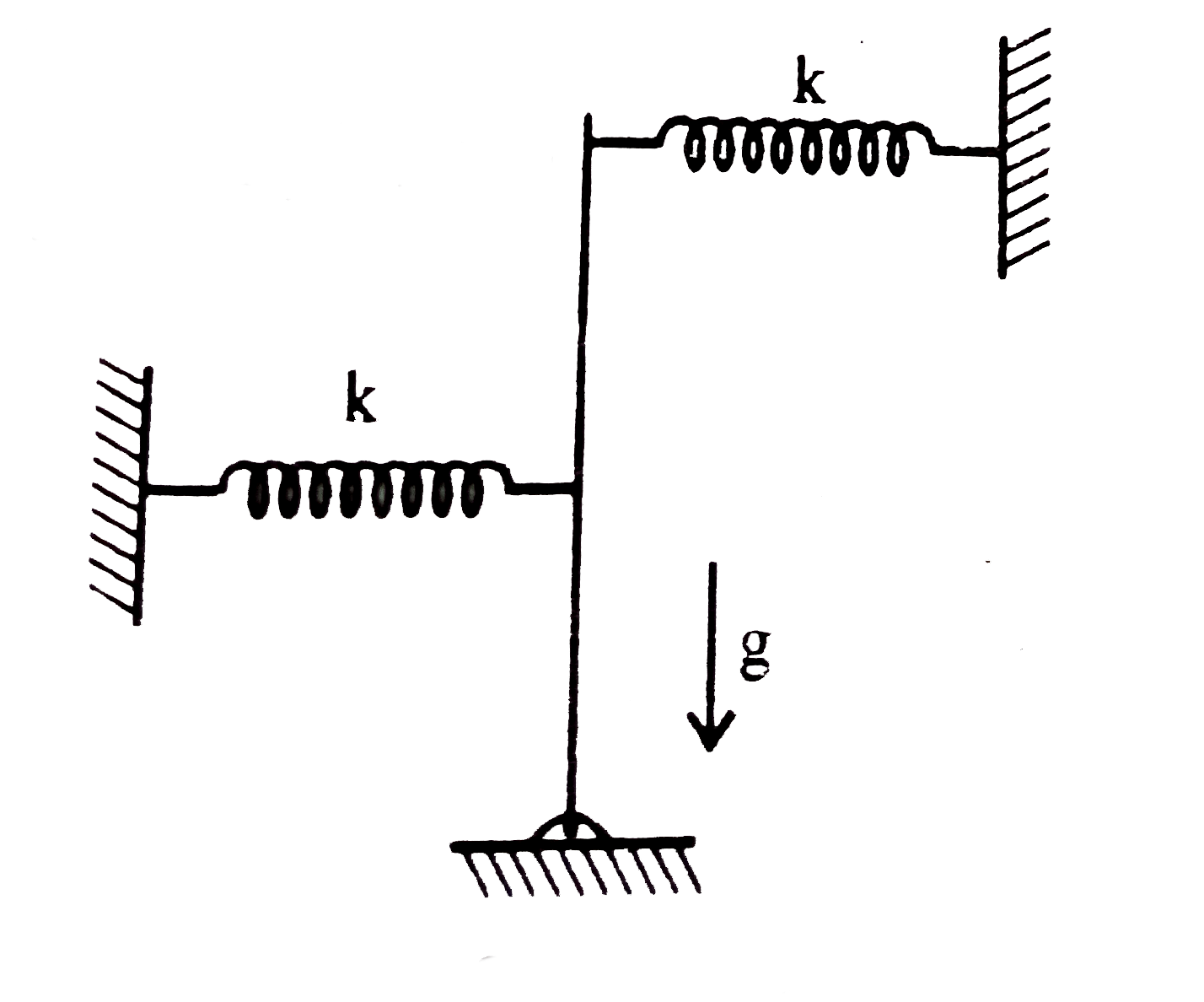 Ak>mg/3LBk>2mg/3LCk>2mg/5LDk=0
Ak>mg/3LBk>2mg/3LCk>2mg/5LDk=0 - Question 3 - Select One
In the figure shown a smooth ring is connected to rod AB, while rod CD passes through ring. At the given instant angular velocity of rod AB about hinge A is 1 rod/s and AC=CB. Instantaneous angular velocity of rod CD about hinge C is
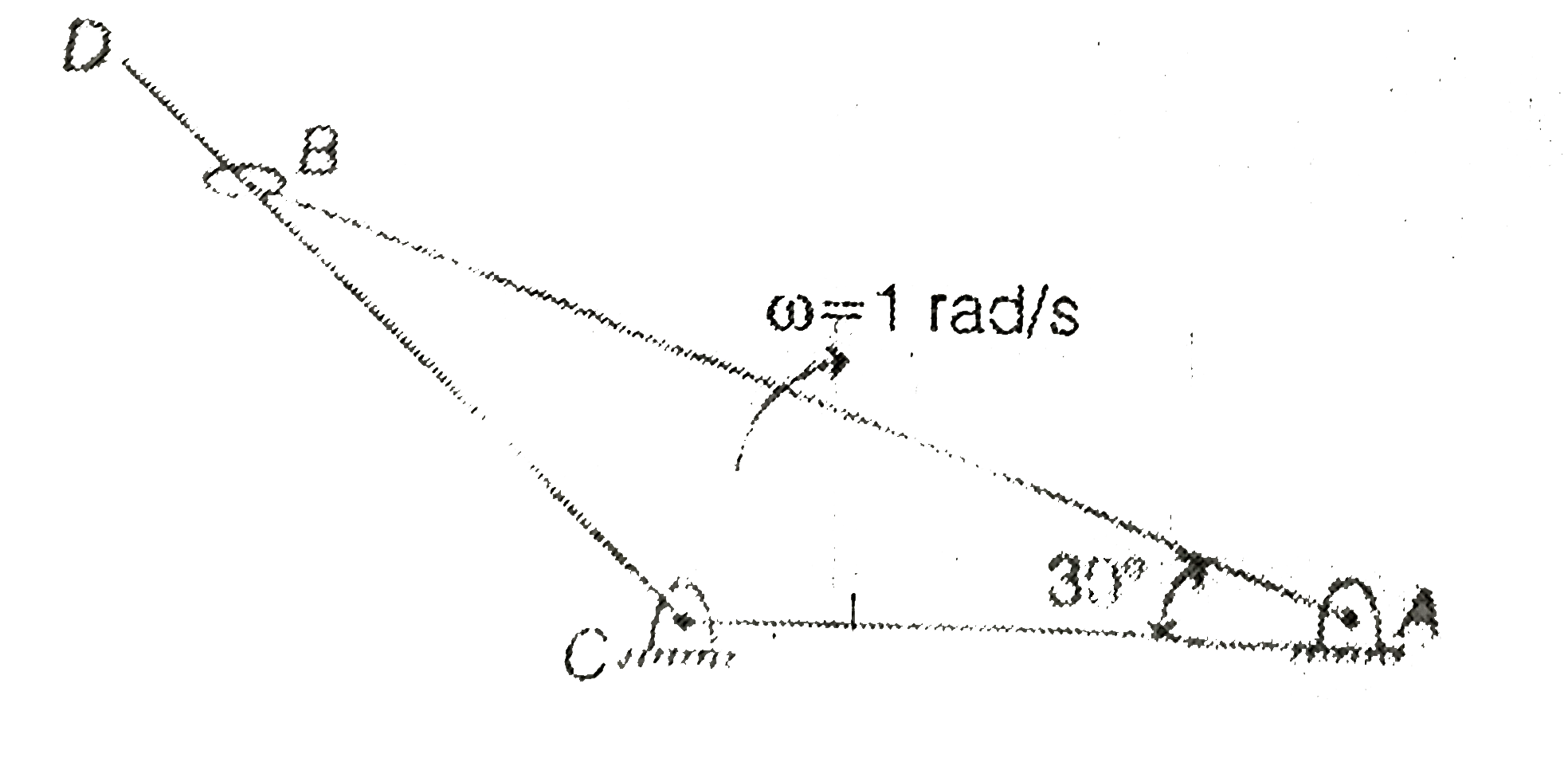 A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/s
A1rad/sB1/2rad/sC√3/2rad/sD3/2rad/s
A particle of mass m in suspended at the lower end of a thin negligible mass. The upper end of the rod is free to rotate in the plane of the page about a horizontal axis passing through the point O. The spring is underformed when the rod is vertical as shown in fig. If the period of oscillation of the system is π√Ln, when it is slightly displaced from its mean position then find n. Take k=9mgKLl2 and g=10m/s2.
 View Solution
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
 View Solution
View SolutionA uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
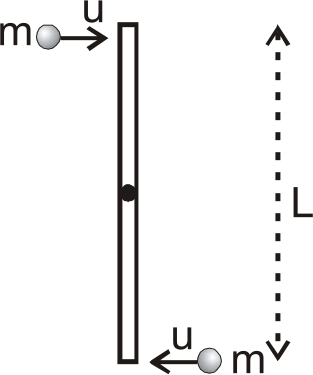 View Solution
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
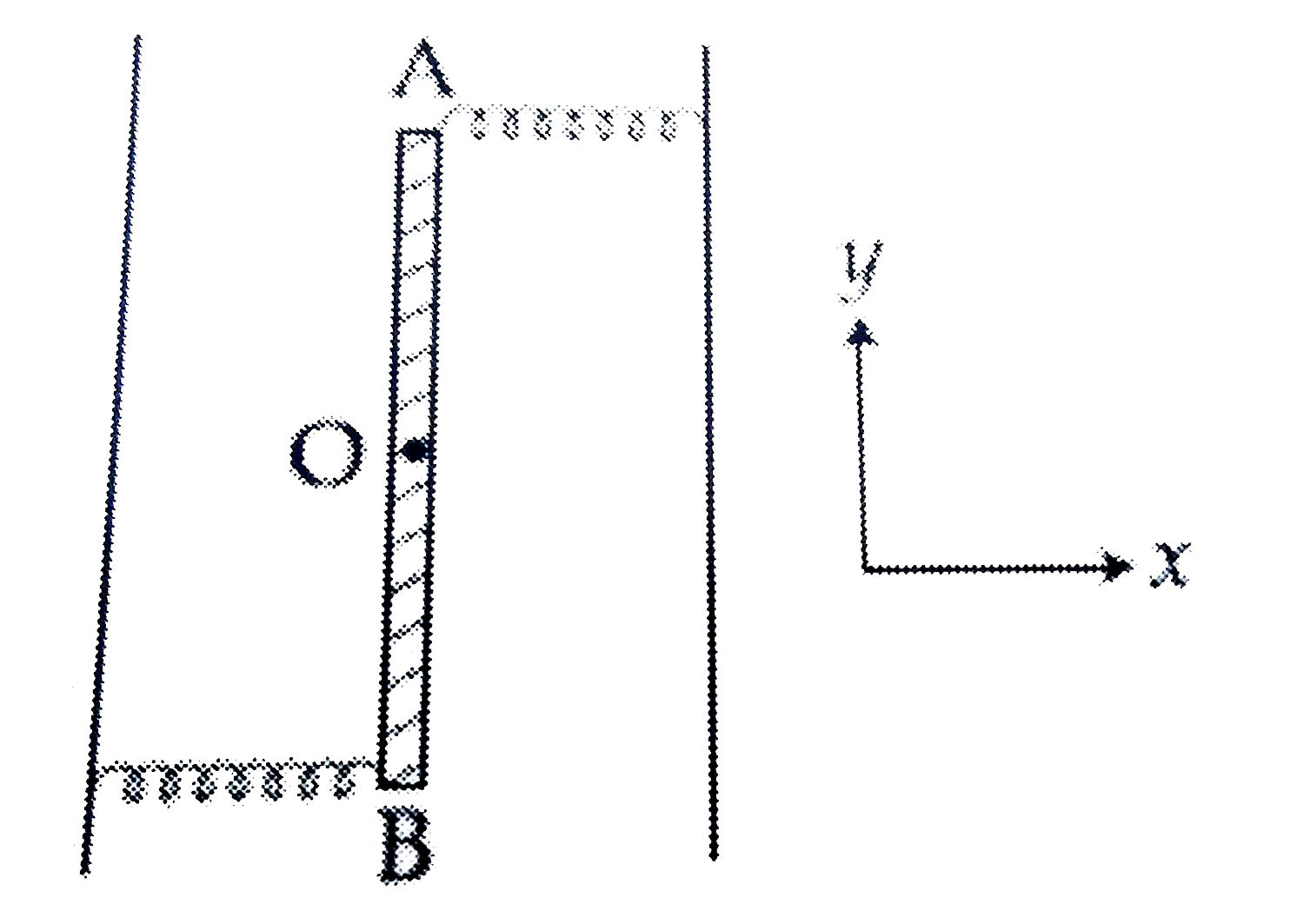 View Solution
View SolutionA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be
 View Solution
View Solution

