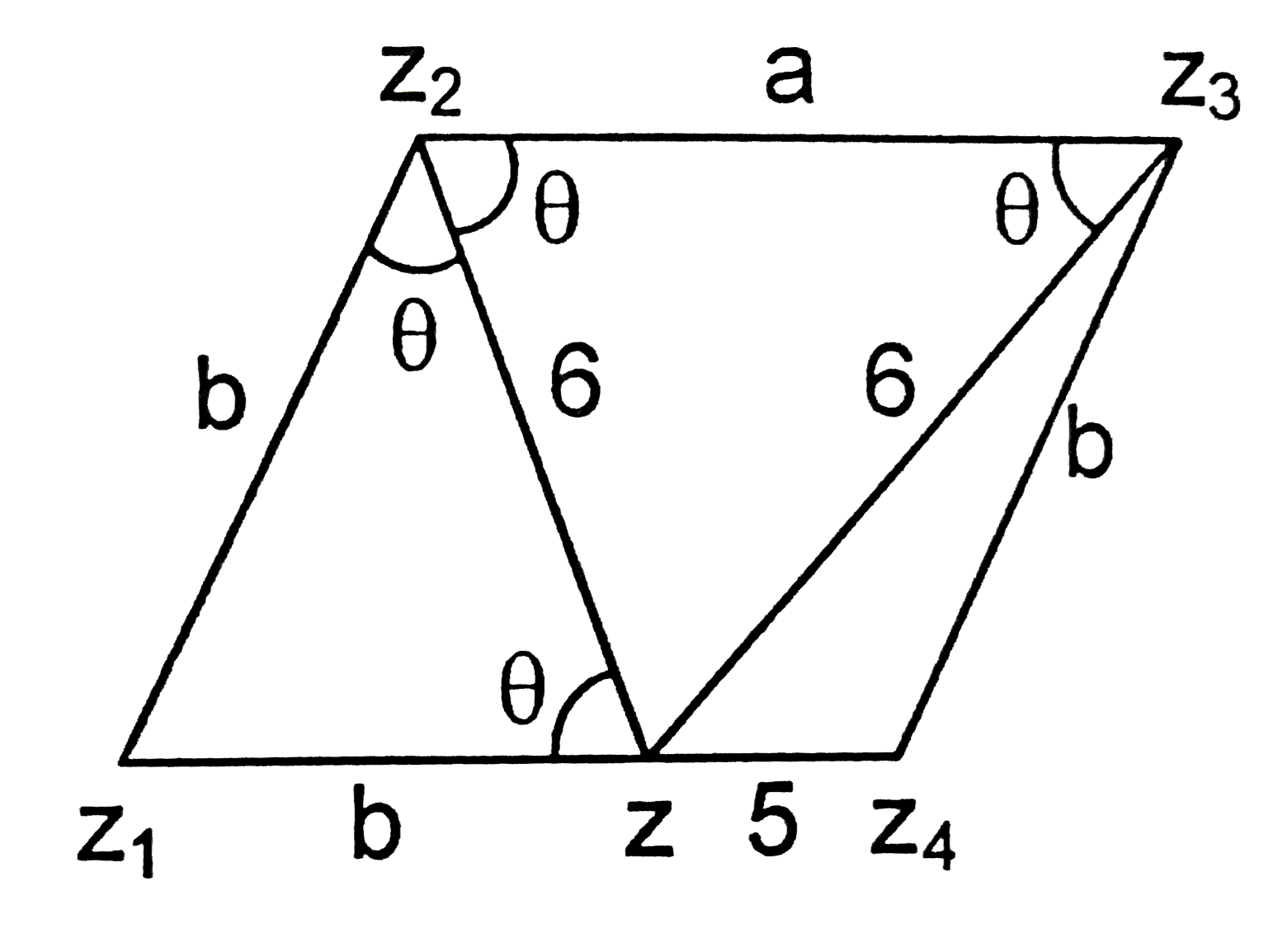
If z1,z2,z3,z4 are complex numbers in an Argand plane satisfying z1+z3=z2+z4. A compex number 'z' lies on the line joining z1 and z4 such that Arg(z−z2z1−z2)=Arg(z3−z2z−z2). It is given that |z−z4|=5,|z−z2|=|z−z3|=6 then
area of triangle formed by z,z1,z2 is 3√7 sq units
area of the triangle formed by z,z3,z4 is 15√73 sq. units
area of the quadrilateral formed by the points z1,z2,z3,z4 taken in orders is (27√7) sq. units
area of the quadrilateral formed by the points z1,z2,z3,z4 taken in order is 27√74 sq. units
The correct Answer is:A, B, C
a=b+5
and b6=6a
⇒ab=36
b2+5b−36=0
⇒b=4
Topper's Solved these Questions
Similar Questions
Knowledge Check
If z1,z2,z3,z4 are two pairs of conjugate complex numbers, then arg(z1z3)+arg(z2z4) is
A0Bπ2C3π4DπLet z1,z2,z3,z4 are distinct complex numbers satisfying |z|=1 and 4z3=3(z1+z2), then |z1−z2| is equal to
A1 or iBior−iC1 or iDior−1If z1,z2 and z3,z4 are two pairs of conjugate complex numbers then arg(z1z4)+arg(z2z3) equals
Aπ2BπC3π2D0
If z1,z2 and z3,z4 are two pairs of conjugate complex numbers then arg(z1z4)+arg(z2z3)=
View SolutionIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
View SolutionIf z1,z2andz3,z4 are two pairs of conjugate complex numbers, hen find the value of a r g(z1/z4)+arg(z2/z3). a
View Solution(z1,z2)and(z3,z4) are two pairs of conjugate complex numbers then arg z1z3+argz2z4 is equal to
View SolutionIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
View Solution
