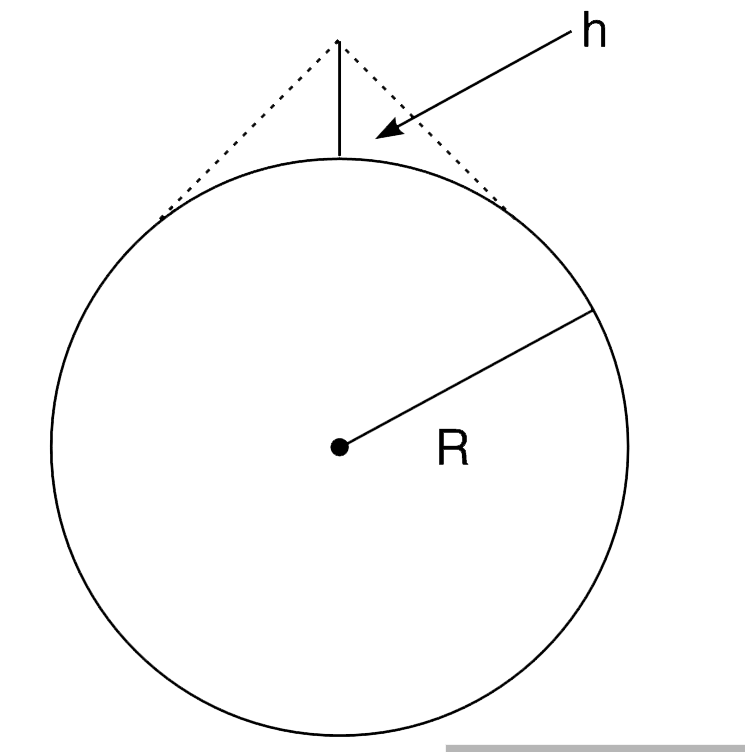
A rope is tightly wound along the equator of a large sphere of radius R. The length of the rope is increased by a small amount $l (< < R)$ and it is pulled away from the surface at a point to make it taut. To what height (h) from the surface will the point rise ?
If the radius of the earth is $R = 6400 k m and l = 10 m m$ , find the value of h. Does the value surprise you.
[For small $θ$ take $\tan θ = θ + \frac{θ^{3}}{3} and \sec θ = 1 + \frac{θ^{2}}{2} . Also take {(2.3)}^{\frac{2}{3}} = 1.74$ ]

Text Solution

Verified by Experts

The correct Answer is: $5.6 m$

Updated on:21/07/2023

A man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is ( $R$ is Radius of the earth )
A $\frac{W}{4}$
B $\frac{W}{2}$
C $W$
D $4 W$
Gravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
A $\frac{- G M}{2 R}$
B $\frac{- G M}{R}$
C $\frac{- G M}{4 R}$
D $- G M$
If body of mass $m$ has to be taken from the surface to the earth to a height $h = 4 R$ , then the amount of energy required is (R = radius of the earth)
A $m g R$
B $\frac{m g R}{5}$
C $\frac{4 m g R}{5}$
D $\frac{m g R}{12}$