In the last problem, the rope is placed on the cylinder as shown. Find maximum tension in the rope.
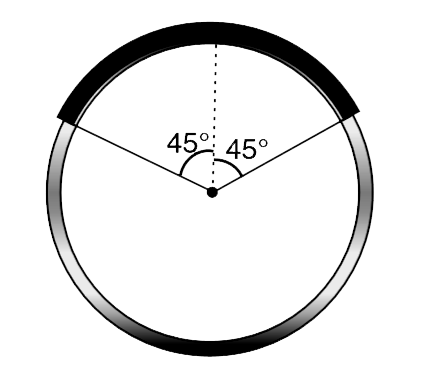
The correct Answer is:Zero
Topper's Solved these Questions
Similar Questions
A uniform rope ABCDE has mass M and it is laid along two incline surfaces (AB and CD) and two horizontal surfaces (BC and DE) as shown in figure. The four parts of the rope AB, BC, CD and DE are of equal lengths. The coefficient of friction (μ) is uniform along the entire surface and is just good enough to prevent the rope from sliding.

(a) Find μ
(b) x is distance measured along the length of the rope starting from point A. Plot the variation of tension in the rope (T) with distance x.
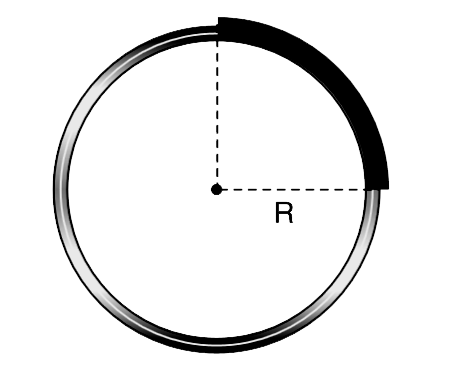
(c) Find the maximum tension in the rope.View SolutionA uniform rope of length πR2 has been placed on fixed cylinder of radius R as shown in the fig. One end of the rope is at the top of the cylinder. The coefficient of friction between the rope and the cylinder is just enough to prevent the rope from sliding. Mass of the rope is M.
(a) At what position, the tension in the rope is maximum?
(b) Calculate the value of maximum tension in the rope.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bus is moving with a constant acceleration a=3g/4 towards right. In the bus, a ball is tied with a rope and is rotated in vertical circle as shown. The tension in the rope will be minimum, when the rope makes an angle θ=_____
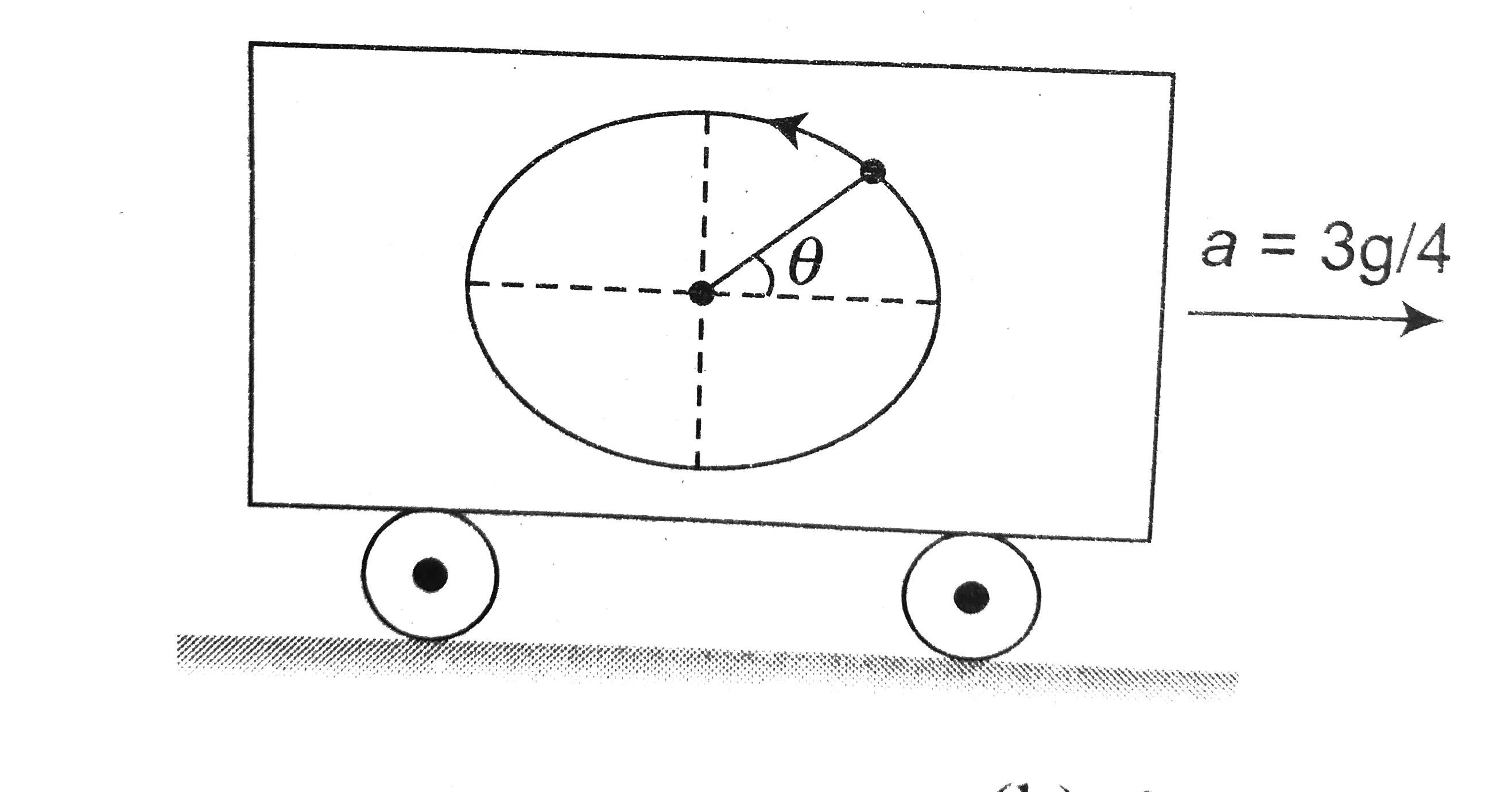 A53∘B37∘C180−53∘D180+37∘
A53∘B37∘C180−53∘D180+37∘ - Question 2 - Select One
An object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 N - Question 3 - Select One
In the previous problem if M=2m, the tension in the middle of the rope is
A3F4B3F5C5F6D7F6
A block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
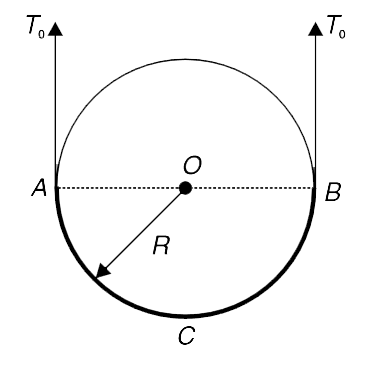
View SolutionA smooth cylinder is fixed with its axis horizontal. Radius of the cylinder is R. A uniform rope (ACB) of linear mass density λ (kg/m) is exactly of length πR and is held in semicircular shape in vertical plane around the cylinder as shown in figure. Two massless strings are connected at the two ends of the rope and are pulled up vertically with force T0 to keep the rope in contact with the cylinder.
(a) Find minimum value of T0 so that the rope does not lose contact with the cylinder at any point.
(b) If T0 is decreased slightly below the minimum value calculated in (a), where will the rope lose contact with the cylinder.
 View Solution
View SolutionA rope of length of 2m is tied between two ends . If the speed of transverse waves propagating in the rope is 4ms−1 and the tension in the rope is 2 N , find the mass of the rope is C.G.S units .
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m, as shown in Fig. 5-35. A horizontal force acts on one end of the rope.

(a) Show that the rope must sag, even if only by an imperceptible amount.
(b) Then, assuming that the sag is negligible, find the acceleration of rope and block.
(c) Find the force on the block from the rope.
(d) Find the tension in the rope at its midpoint.View SolutionA uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
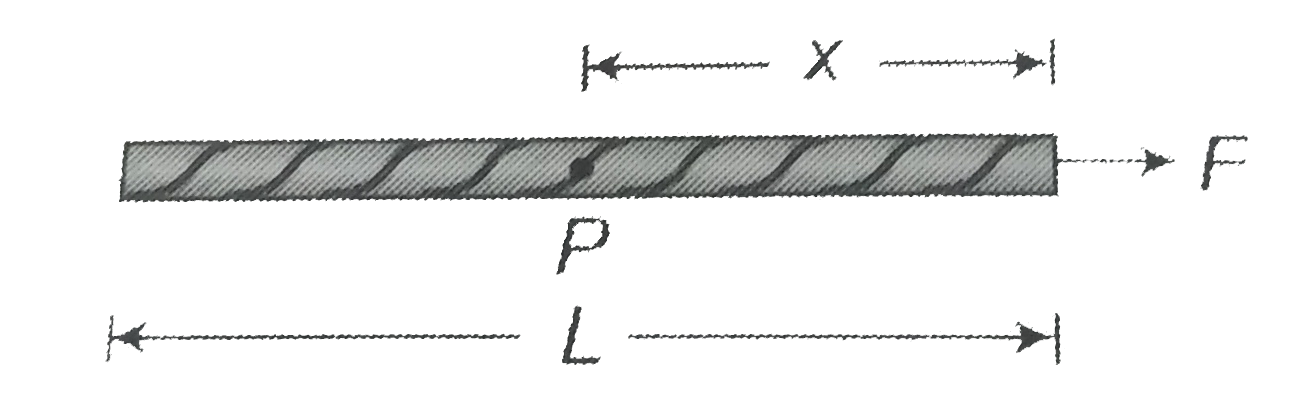 View Solution
View Solution

