A uniform rope of length πR2 has been placed on fixed cylinder of radius R as shown in the fig. One end of the rope is at the top of the cylinder. The coefficient of friction between the rope and the cylinder is just enough to prevent the rope from sliding. Mass of the rope is M.
(a) At what position, the tension in the rope is maximum?
(b) Calculate the value of maximum tension in the rope.
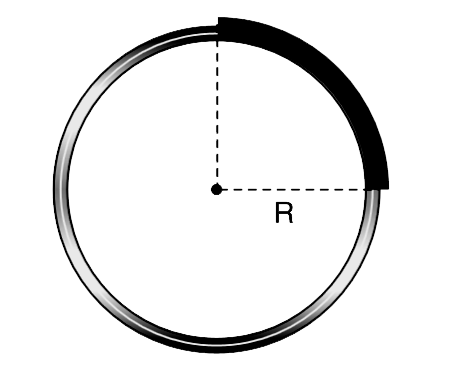
The correct Answer is:(a) θ=45∘ from vertical diameter .
(b) Tmax=2(√2−1π)Mg
Topper's Solved these Questions
Similar Questions
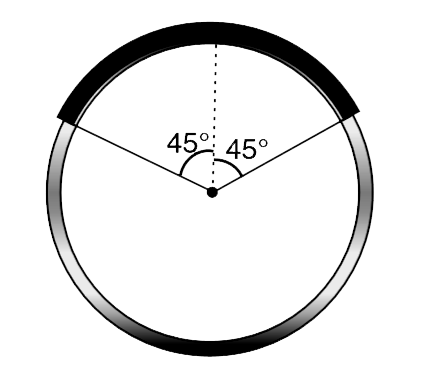
In the last problem, the rope is placed on the cylinder as shown. Find maximum tension in the rope.
View SolutionA rope lies on a table such that a part of it hangs down the table, when the length of hanging part is 1/3 of entire length the rope just begins to slide. The coefficient of friction between the rope and the table is:-
View Solution
Knowledge Check
A rope lies on atable such that a part of it hangs down the table, when the length of hanging part is 1/3 of entire length the rope just begins to slide. The coefficient of friction between the rope and the table is:-
A2/3B1/2C1/3D1/6A unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
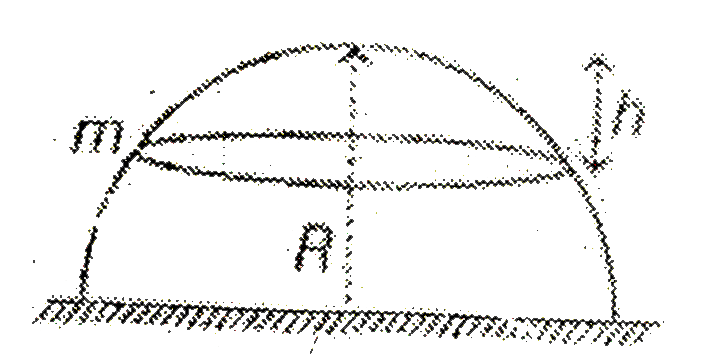 Amg2πBmg2C√3mg2D√3mg2π
Amg2πBmg2C√3mg2D√3mg2πA rope of length L and mass M is being pulled on a rought horizontal floor by a contact horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rop. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rop is
AMg4B2Mg5CMg8DMg2
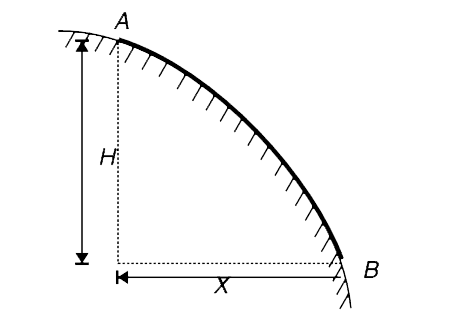
A uniform rope has been placed on a sloping surface as shown in the figure. The vertical separation and horizontal separation between the end points of the rope are H and X respectively. The friction coefficient (μ) is just good enough to prevent the rope from sliding down. Find the value of μ.
View SolutionA rope of length (π2+1) R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is λ . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass (M0) of a block that can be tied to the end B of the rope so that the string does not break.
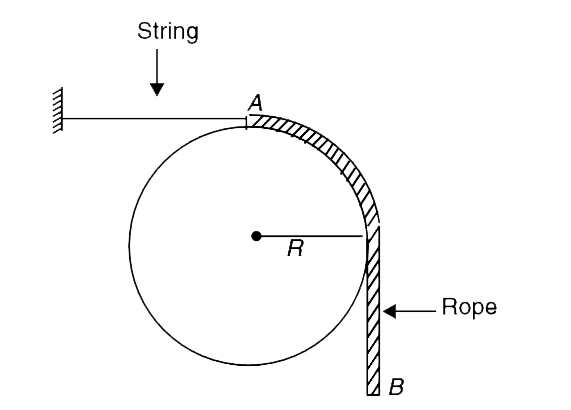
View SolutionA rope of length L and mass M is being pulled on a rough horizontal floor by a contact horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rope. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rope is
View SolutionIf the coefficient of static friction between a table and a uniform massive rope is μ, what fraction of the rope can hang over the edge of a table without the rope sliding.
View SolutionA uniform rope ABCDE has mass M and it is laid along two incline surfaces (AB and CD) and two horizontal surfaces (BC and DE) as shown in figure. The four parts of the rope AB, BC, CD and DE are of equal lengths. The coefficient of friction (μ) is uniform along the entire surface and is just good enough to prevent the rope from sliding.

(a) Find μ
(b) x is distance measured along the length of the rope starting from point A. Plot the variation of tension in the rope (T) with distance x.
(c) Find the maximum tension in the rope.
View Solution
