A particle P is attached to two fixed points O1 and O2 in a horizontal line, by means of two ight inextensible strings of equal length l. It is projected with a velocity just sufficient to make it describe a circle, in a vertical plane, without the strings getting slack and with the angle<O2O1P=<O1O2P=θ. When the particle is at its lowest point, the string O2P breaks and the subsequent path of the particle was found to be a circle of radius l cosθ. Find θ.
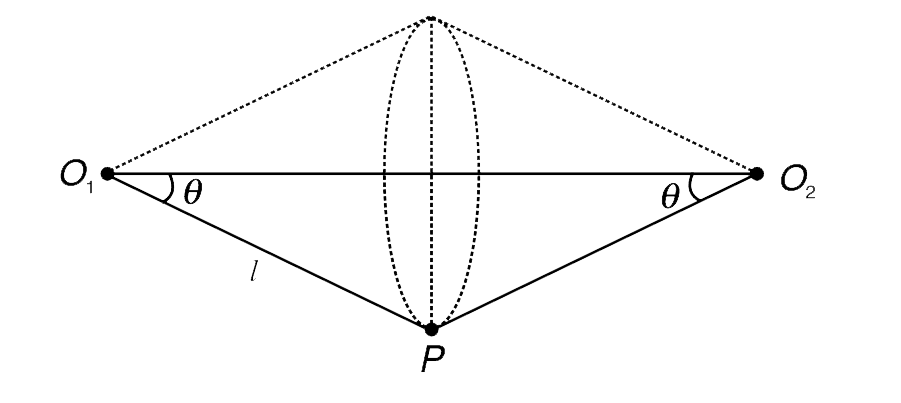
The correct Answer is:θ=tan−1(1√5)
Topper's Solved these Questions
Similar Questions
A particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?

View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
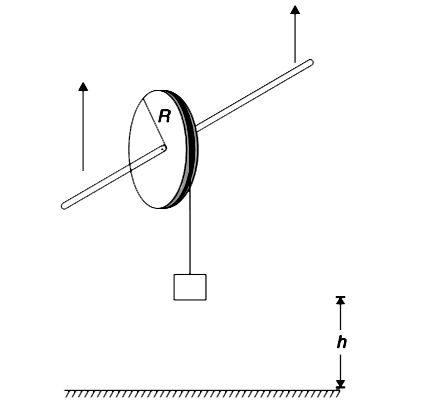
View SolutionThere are two holes O_(1) and O_(2) in a tank of height H. The water emerging from O_(1) and O_(2) strikes the ground at the same points as shows in fig. Then:
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed 2 sqrt((2g)/(h)) where AB = h
View SolutionA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity sqrt(7gl//2) . The string will slack after swinging through an angle equal to
View SolutionThere are two holes O_(1) " and " O_(2) in a tank of height H. The water emerging from O_(1) " and " O_(2) strikes the ground at the same points, as shown in figure. Then
View SolutionStatement-1 : O−2 and O+2 are paramagnetic .
and
Statement-2 : Bond order of O+2 and O−2 is same .
View SolutionA heavy particle of weight w, attached to a fixed point by a light inextensible string describes a circle in a vertical plane. The tension in the string has the values nw and mw respectively when the particle is at the highest and lowest points in the path. Then :
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u = sqrt((2 + sqrt(3))ag) . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionCircle O1≅Circle O2, If radius of circle O1=6cm then diameter of circle O2 is ________
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
View SolutionTwo circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
View SolutionBalance the following equation:
P+O2→P2O5
View Solution
