A force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
0.5J
2.5J
5J
10 J
The correct Answer is:B
To find the potential energy stored in the spring when a force is applied, we can follow these steps:
1. Identify the Given Values:
- Force (F) = 10 N
- Spring constant (k) = 20 N/m
2. Use Hooke's Law to Find Compression (x):
Hooke's Law states that the force applied to a spring is proportional to its compression or extension:
F=k⋅x
Rearranging this gives:
x=Fk
Substituting the known values:
x=10N20N/m=0.5m
3. Calculate the Potential Energy (U) Stored in the Spring:
The potential energy stored in a spring is given by the formula:
U=12kx2
Substituting the values of k and x:
U=12⋅20N/m⋅(0.5m)2
U=12⋅20⋅0.25
U=10⋅0.25=2.5J
4. Conclusion:
The potential energy stored in the spring is:
U=2.5J
- Force (F) = 10 N
- Spring constant (k) = 20 N/m
Hooke's Law states that the force applied to a spring is proportional to its compression or extension:
F=k⋅x
Rearranging this gives:
x=Fk
Substituting the known values:
x=10N20N/m=0.5m
The potential energy stored in a spring is given by the formula:
U=12kx2
Substituting the values of k and x:
U=12⋅20N/m⋅(0.5m)2
U=12⋅20⋅0.25
U=10⋅0.25=2.5J
The potential energy stored in the spring is:
U=2.5J
Topper's Solved these Questions
Similar Questions
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA spring of force constant 4000N/m when stretched by 8 cm, the potential energy stored in it will be?
View Solution
Knowledge Check
A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .
 A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A(mg)24kB(mg)22kC(mg)28kD(mg)2k.Two masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length
 Aenergy of smaller body will be 20 JBenergy of smaller body will be 40 JCenergy of smaller body will be 10 JDenergy of both the bodies will be same
Aenergy of smaller body will be 20 JBenergy of smaller body will be 40 JCenergy of smaller body will be 10 JDenergy of both the bodies will be sameWhen a spring is stretched by 10 cm, the potential energy stored is E. When the spring is stretched by 10 cm more, the potential energy stored in the spring becomes
A2EB4EC6ED10E.
A vertical spring supports a beaker containing some water in it. Water slowly evaporates and the compression in the spring decreases. Where does the elastic potential energy stored in the spring go?
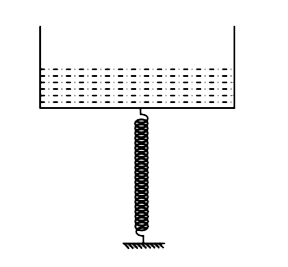
View SolutionWhen a spring is stretched by 10 cm, the potential energy stored is E. When the spring is stretched by 10 cm more, the potential energy stored in the spring becomes
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View SolutionThe potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8cm, the potential energy stored in it is
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View Solution
