A heavy rope of mass m and length 2L is hanged on a smooth little peg with equal lengths on two sides of the peg. Right part of the rope is pulled a little longer and released. The rope begins to slide under the action of gravity. There is a smooth cover on the peg (so that the rope passes through the narrow channel formed between the peg and the cover) to prevent the rope from whiplashing.
(a) Calculate the speed of the rope as a function of its length (x) on the right side.
(b) Differentiate the expression obtained in (a) to find the acceleration of the rope as a function of x.
(c) Write the rate of change of momentum of the rope as a function of x. Take downward direction as positive
(d) Find the force applied by the rope on the peg as a function of x.
(e) For what value of x, the force found in (d) becomes zero? What will happen if there is no cover around the peg ?
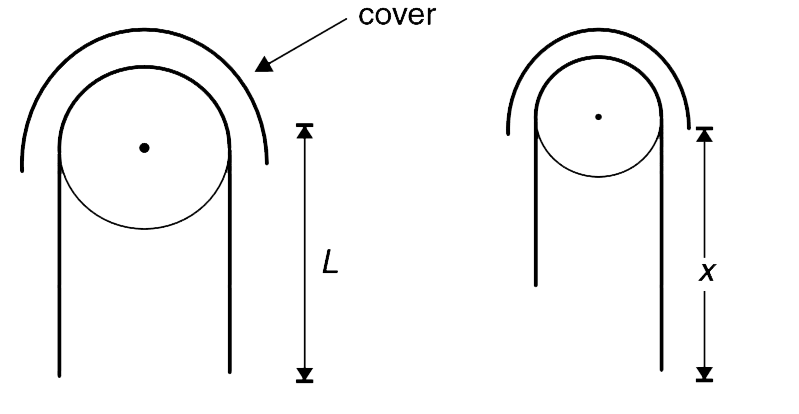
The correct Answer is:(a) v=√gL(x−L)
(b) a=gL(x−L)
(c) dpdt=2mg(x−LL)2
(d) F=mg[1−2(x−LL)2]
(e) x=L+L√2
Step by step video, text & image solution for A heavy rope of mass m and length 2L is hanged on a smooth little peg with equal lengths on two sides of the peg. Right part of the rope is pulled a little longer and released. The rope begins to slide under the action of gravity. There is a smooth cover on the peg (so that the rope passes through the narrow channel formed between the peg and the cover) to prevent the rope from whiplashing. (a) Calculate the speed of the rope as a function of its length (x) on the right side. (b) Differentiate the expression obtained in (a) to find the acceleration of the rope as a function of x. (c) Write the rate of change of momentum of the rope as a function of x. Take downward direction as positive (d) Find the force applied by the rope on the peg as a function of x. (e) For what value of x, the force found in (d) becomes zero? What will happen if there is no cover around the peg ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View SolutionA uniform rod of mass M and length 2L lies on a smooth horizontal table. There is a smooth peg O fixed on the table. One end of the rod is kept touching the peg as shown in the figure. An impulse J is imparted to the rod at its other end. The impulse is horizontal and perpendicular to the length of the rod. Find the magnitude of impulse experienced by the peg.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rope of length l and mass m lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small part of the rope having over the edge. The rope starts sliding from rest under the weight of the over hanging end. The velocity of the rope when the length of the hanging part is . x
A√gxlB√gx2lCgxlDgx2l - Question 2 - Select One
A uniform rope so lies on a table that part of it lays over. The rope begins to slide when the length of hanging part is 25% of entire length. The co-efficient of friction between rope and table is
A0.33B0.25C0.5D0.2 - Question 3 - Select One
A uniform rope of length 'L and linear density 'μ' is on a smooth horizontal table with a length 'I' lying on the table. The wrok done in pulling the hanging part on to the table is
Aμg(L−l)22Bμg(L−l)22l2Cμg(L−l)22L2DμgL2(L−l)
A uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
 View Solution
View SolutionPEG stand for
View SolutionA uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
 View Solution
View SolutionA rope lies on atable such that a part of it hangs down the table, when the length of hanging part is 1/3 of entire length the rope just begins to slide. The coefficient of friction between the rope and the table is:-
View SolutionA uniform rope of length l lies on a table if the coefficient of friction is , then the maximum length l, of the part of this rope which can over hang from the edge of the table without sliding down is -
View Solution

