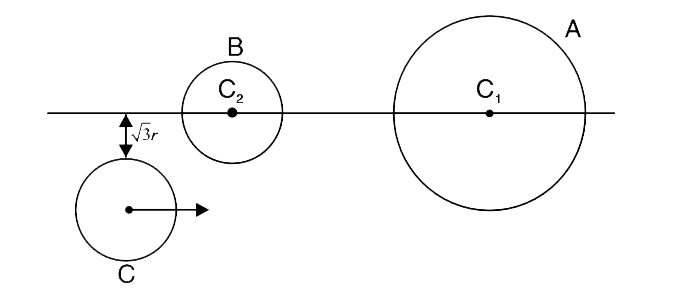
Disc A of radius R is lying flat on a horizontal surface. Disc B is also at rest. Disc C, which is identical to B is traveling along the surface with its velocity parallel to the line joining the centre C1andC2 of the discs A and B. The distance between the line C1C2 and the line of motion of centre of disc C is √3r , where r is radius of both B and C. Impact of C with B is completely elastic. Subsequently it is observed that both B and C just miss hitting the disc A. Find the radius (R) of A in terms of r.
The correct Answer is:R=(√3+1√3−1)r
Step by step video, text & image solution for Disc A of radius R is lying flat on a horizontal surface. Disc B is also at rest. Disc C, which is identical to B is traveling along the surface with its velocity parallel to the line joining the centre C_(1) and C_(2) of the discs A and B. The distance between the line C_(1)C_(2) and the line of motion of centre of disc C is sqrt(3)r , where r is radius of both B and C. Impact of C with B is completely elastic. Subsequently it is observed that both B and C just miss hitting the disc A. Find the radius (R) of A in terms of r. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
 03:52View Solution
03:52View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .04:28View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals ilts radius. Find the distance of the line from the centre.
03:01View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
05:50View SolutionTwo identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
02:53View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance (R)/(2) from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
05:26View SolutionOn the flat surface of a disc of radius a a small circular hole of radius b is made with its centre at a distance c from the centre of the disc. If mass of the whole un cut disc is M, calculate the moment of inertia of the holed disc about the axis of the circular hole. [(1)/(2)[a^(2) + 2c^(2)- (b^(4))/(a^(2))]]
02:39View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be
 02:54View Solution
02:54View SolutionFrom a uniform disc of radius R, a circular disc of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of original disc. Locate the centre of gravity of the resultant flat body.
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc equals to its radius. Find the distance of the line from the centre.
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc is equal to its radius. Find the distance of the line from the centre of the disc.
03:11View SolutionThree identical discs, A, B and C rest on a smooth horizontal plane as shown in figure. The disc A is set in motion with velocity v along the perpendicular bisector of the line BC joining the centres of the stationary discs. The distance BC between the centre of stationary discs B and C is n times the diameter .d. of each disc. At what value of n will the disc A recoil, stop and move on after elastic collision?
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc is equal to its radius. Find the distance of the line from the centre of the disc.
View SolutionThe radius of gyration of a uniform disc about a line perpendicular to the disc is equal to its radius. Find the distance of the line from the centre of the disc.
02:27View SolutionA disc of radius 10 cm is rolling on a horizontal surface. The velocity of its centre is 4ms−1 and angular velocity of rotation of the disc is 50 rads−1. What is the distance (in cm) of instantaneous axis of rotation from the centre of the disc ?
04:54View Solution

