A small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0.

(a) The velocity of the centre of the disc becomes zero for the first time at time t0. Find t0
(b) Find speed of the small body at time t03
The correct Answer is:(a) t0=2πRV0
(b) V02
Step by step video, text & image solution for A small body of mass m is at rest inside a narrow groove carved in a disc. Groove is a circle of radius R concentric to the disc. Mass of the disc is also m . The disc lies on a smooth horizontal floor. The small body is given a sharp impulse so that it acquires a tangential velocity Vo at time t = 0. (a) The velocity of the centre of the disc becomes zero for the first time at time t_(0). Find t_(0) (b) Find speed of the small body at time (t_(0))/(3) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The speed of each ball relative to the ground just after they leave the disc is
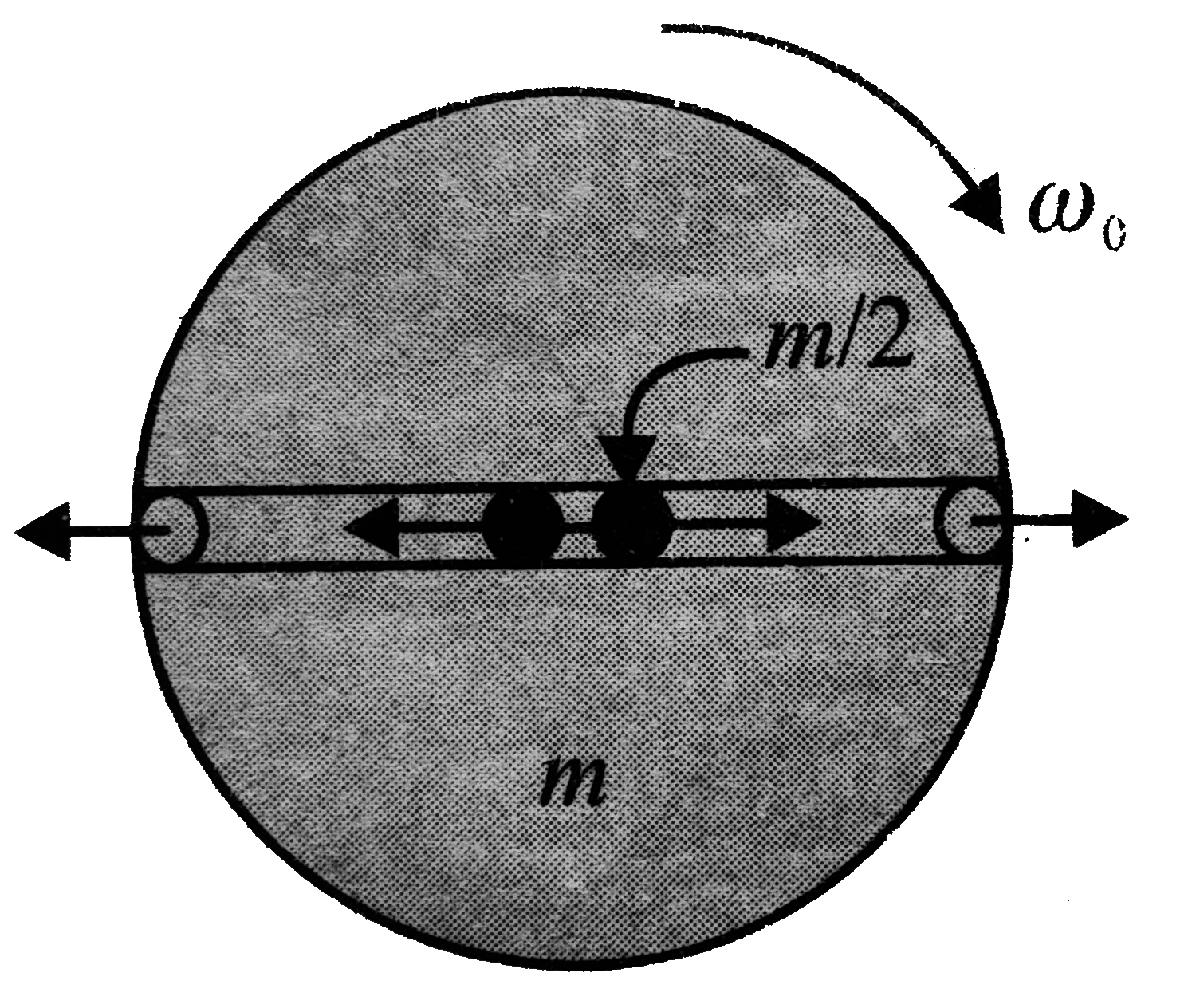
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m//2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity omega_(0) and released. The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc is
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
View SolutionA uniform disc of mass 'm' and radius R is placed on a smooth horizontal floor such that the plane surface of the disc in contact with the floor . A man of mass m//2 stands on the disc at its periphery . The man starts walking along the periphery of the disc. The size of the man is negligible as compared to the size of the disc. Then the center of disc.
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance (R)/(2) from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
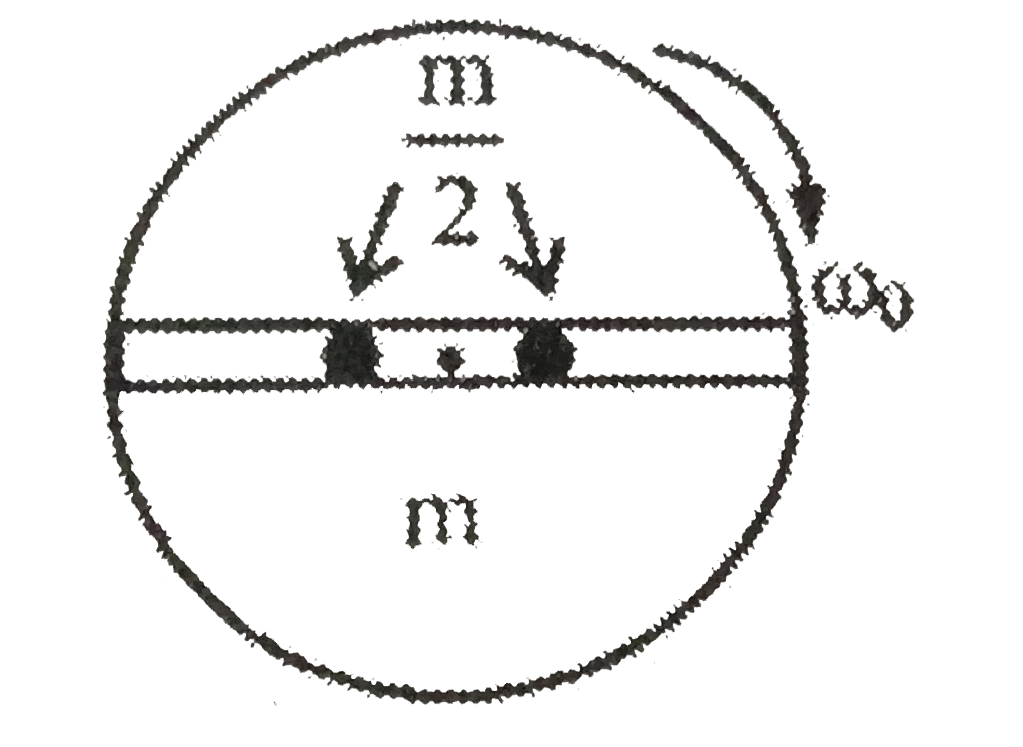
View SolutionA disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity ω0 and released. The angular speed of the disc when the balls reach the end of the disc is -
View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View SolutionA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View Solution
