A small asteroid is at a large distance from a planet and its velocity makes an angle phi(cancel(=)0) with line joining the asteroid to the centre of the planet. Prove that such an asteroid can never fall normally on the surface of the planet.

Step by step video, text & image solution for A small asteroid is at a large distance from a planet and its velocity makes an angle phi(cancel(=)0) with line joining the asteroid to the centre of the planet. Prove that such an asteroid can never fall normally on the surface of the planet. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
An asteroid was fast approaching the earth. Scientists fired a rocket which hit the asteroid at a distance of 5 R from the centre of the earth (R = radius of the earth). mmediately after the hit the asteroid’s velocity (V0) was making an angle of θ=30∘ with the line joining the centre of the earth to the asteroid. The asteroid just grazed past the surface of the earth. Find V0 [Mass of the earth = M]
 View Solution
View Solution
A small asteroid is approaching a planet of mass M and radius R from a large distance. Initially its velocity (u) is along a tangent to the surface of the planet. It fall on the surface making an angle of 302 with the vertical. Calculate u.View Solution
Knowledge Check
- Question 1 - Select One
If the angular velocity of a planet about its own axis is halved, the distance of geostationary satellite of this planet from the centre of the centre of the planet will become
A(2)1/2 timesB(2)3/2timesC(2)2/3 timesD4 times - Question 2 - Select One
A tunnel is dug along a diameter of the planet. A particle is dropped into it at the surface. The particle reaches the centre of the planet with speed v. If ve is the escape velocity from the surface fo the planet, then-
A√2v=veBv=veCve=√3vDve=√5v - Question 3 - Select One
If the radius of a planet is R and its density is ρ , the escape velocity from its surface will be
Ave∝ρRBve∝√ρRCve∝√ρRDve∝1√ρR
The earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p0r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p0.
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
 View Solution
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
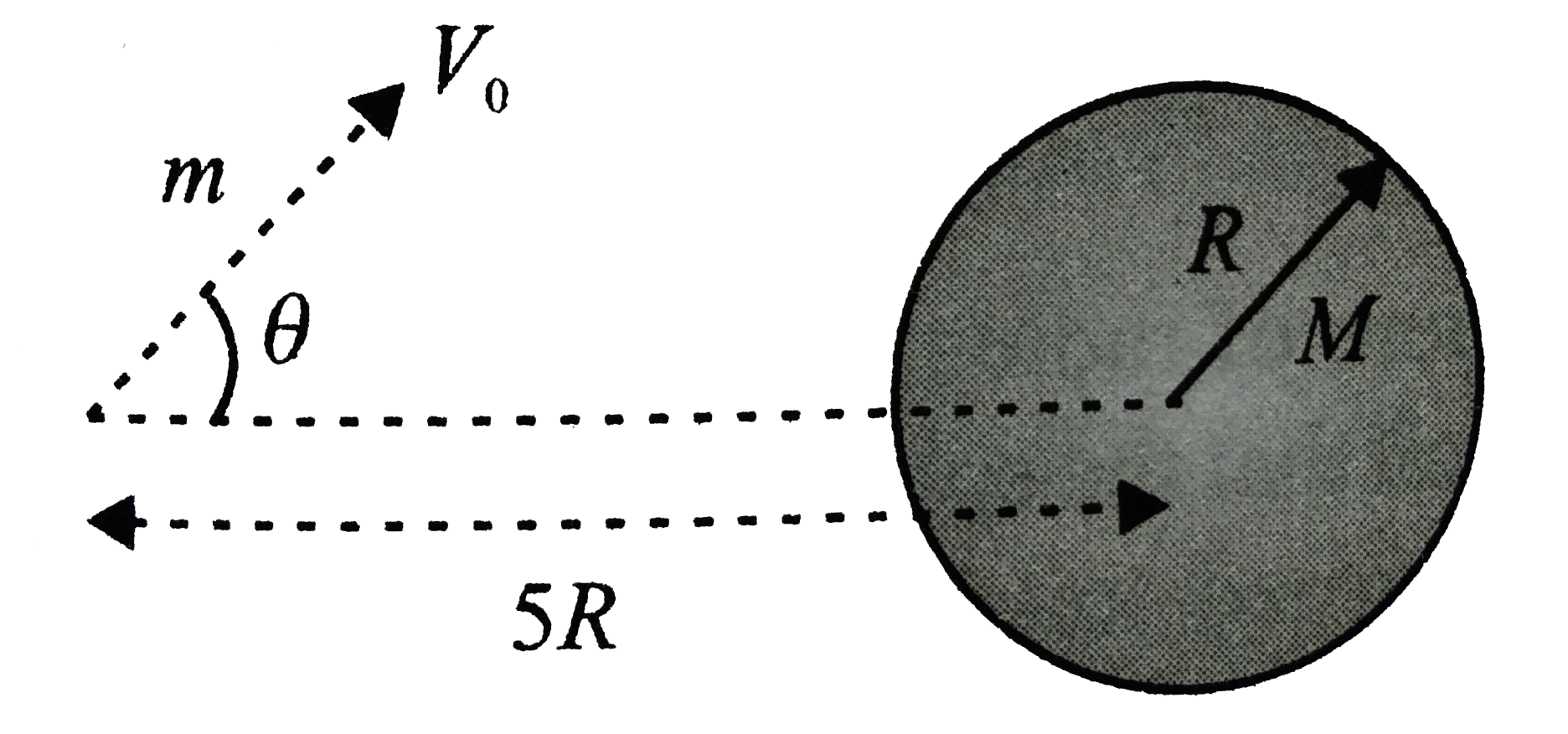 View Solution
View SolutionA space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?
View SolutionA space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?
View Solution

