During a painting process, a thin, flat tape of width b (dimension perpendicular to the plane of the figure) is pulled through a paint filled channel of length L. The density and viscosity of the paint liquid is and respectively. The tape is pulled at a constant speed v and width of the channel is h. Find the minimum force needed to pull the tape.

Step by step video & image solution for During a painting process, a thin, flat tape of width b (dimension perpendicular to the plane of the figure) is pulled through a paint filled channel of length L. The density and viscosity of the paint liquid is rho and eta respectively. The tape is pulled at a constant speed v and width of the channel is h. Find the minimum force needed to pull the tape. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
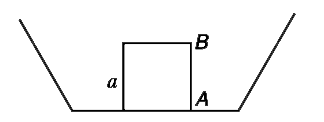
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
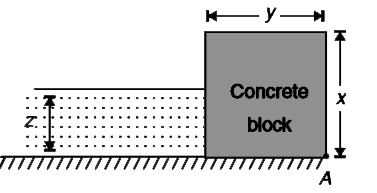
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
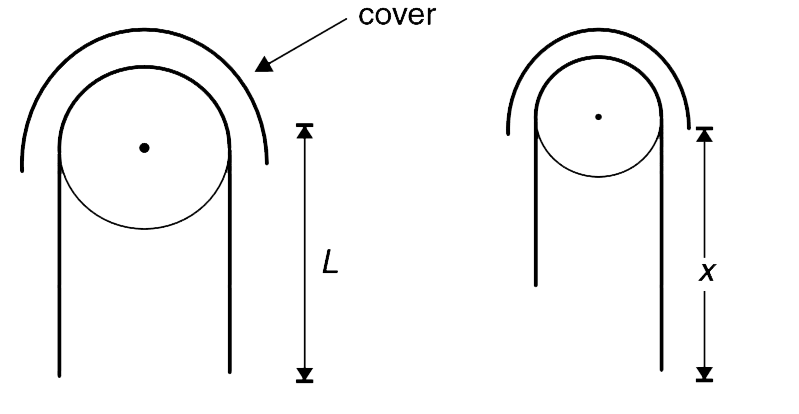
View SolutionA heavy rope of mass m and length 2L is hanged on a smooth little peg with equal lengths on two sides of the peg. Right part of the rope is pulled a little longer and released. The rope begins to slide under the action of gravity. There is a smooth cover on the peg (so that the rope passes through the narrow channel formed between the peg and the cover) to prevent the rope from whiplashing.
(a) Calculate the speed of the rope as a function of its length (x) on the right side.
(b) Differentiate the expression obtained in (a) to find the acceleration of the rope as a function of x.
(c) Write the rate of change of momentum of the rope as a function of x. Take downward direction as positive
(d) Find the force applied by the rope on the peg as a function of x.
(e) For what value of x, the force found in (d) becomes zero? What will happen if there is no cover around the peg ?
View Solution
Knowledge Check
In a thin rectangular metallic strip a constant current I flows along the positive x−direction,asshown∈thefigure.The≤n>h,whandthick≠ssofthestriparel, w and d,respectively.<br>Auniformmag≠ticfieldvec(B)isappliedonthestripalongthepositivey- direction.Due→this,thechar≥carriersexperiencea≠tdef≤ctionalongthez- direction.Thisrest–s∈auμlationofchar≥carriersonthesurfacePQRSansdapperanceofequalandoppositechar≥sonthefaceopposite→PQRS.Apotentiald⇔erencealongthez-directionisthusdeveloped.Char≥auμlationcontiuesuntillthemag≠ticforceisbalancedbythee≤ctricforce.Thecurrentisas∑ed→beuniformlydistributedonthecross−sectionofthestripandcarriedbye≤ctrons.<br>Consrtwod⇔erentmηllicstrips(1 and 2)ofthesamematerial.Their≤n>hsarethesame,whsarew_(1) and w_(2)andthick≠ssared_(1) and d_(2)respectively.Twop∮sK and Maresymmetricallylocatedontheoppositefacesparal≤l→the x-ypla≠(seefigure).V_(1) and V_(2)arethepotentiald⇔erencesbetweenK and M∈strips 1 and 2,respectively.Then,foragivencurrentIflow∈gthroughthem∈agivenmag≠ticfieldstren>hB, the correct statement(s) is (are)
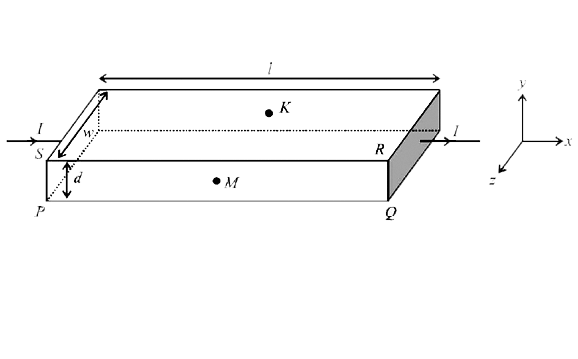 AIf w1=w2andd1=2d2,thenV2=2V1BIf w1=w2andd1=2d2,thenV2=V1CIf w1=2w2andd1=d2,thenV2=2V1DIf w1=2w2andd1=2d2,thenV2=V1
AIf w1=w2andd1=2d2,thenV2=2V1BIf w1=w2andd1=2d2,thenV2=V1CIf w1=2w2andd1=d2,thenV2=2V1DIf w1=2w2andd1=2d2,thenV2=V1In a thin rectangular metallic strip a constant current I flows along the positive x−direction,asshown∈thefigure.The≤n>h,whandthick≠ssofthestriparel, w and d,respectively.<br>Auniformmag≠ticfieldvec(B)isappliedonthestripalongthepositivey- direction.Due→this,thechar≥carriersexperiencea≠tdef≤ctionalongthez- direction.Thisrest–s∈auμlationofchar≥carriersonthesurfacePQRSansdapperanceofequalandoppositechar≥sonthefaceopposite→PQRS.Apotentiald⇔erencealongthez-directionisthusdeveloped.Char≥auμlationcontiuesuntillthemag≠ticforceisbalancedbythee≤ctricforce.Thecurrentisas∑ed→beuniformlydistributedonthecross−sectionofthestripandcarriedbye≤ctrons.<br>Consrtwod⇔erentmηllicstrips(1 and 2)ofsamedimensionsn_(1) and n_(2),repectrively.Strip1isplaced∈mag≠ticfieldB_(1)andstrip2isplaced∈mag≠ticfieldB_(2),⊥halongpositive y- directions.Then V_(1) and V_(2)arethepotentiald⇔erencesdevelopedbetweenK and M∈strips1and2,respectively.As∑∈gtˆthecurrentI is the same for both the strips, the correct option(s) is (are)
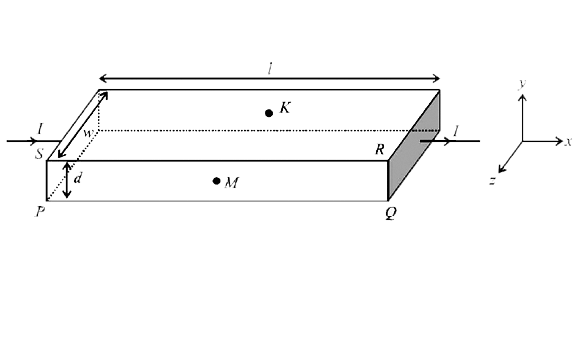 AIf B1=B2andn1=2n2,thenV2=2V1BIf B1=B2andn1=2n2,thenV2=V1CIf B1=2B2andn1=2n2,thenV2=0.5V1DIf B1=2B2andn1=2n2,thenV2=V1
AIf B1=B2andn1=2n2,thenV2=2V1BIf B1=B2andn1=2n2,thenV2=V1CIf B1=2B2andn1=2n2,thenV2=0.5V1DIf B1=2B2andn1=2n2,thenV2=V1
A thin plate of large area is placed midway in a gap of height h filled with oil of viscosity and the plate is pulled at constant velocity vby applying the same drag force on the plate. If a lighter oil of viscosity η is then substituted in the gap. it is found that for the velocity v, and the same drag force as previous case the plate is located unsymmetrically in the gap but parallel to the walls. Find η in terms of distance from nearer wall to the plane y.
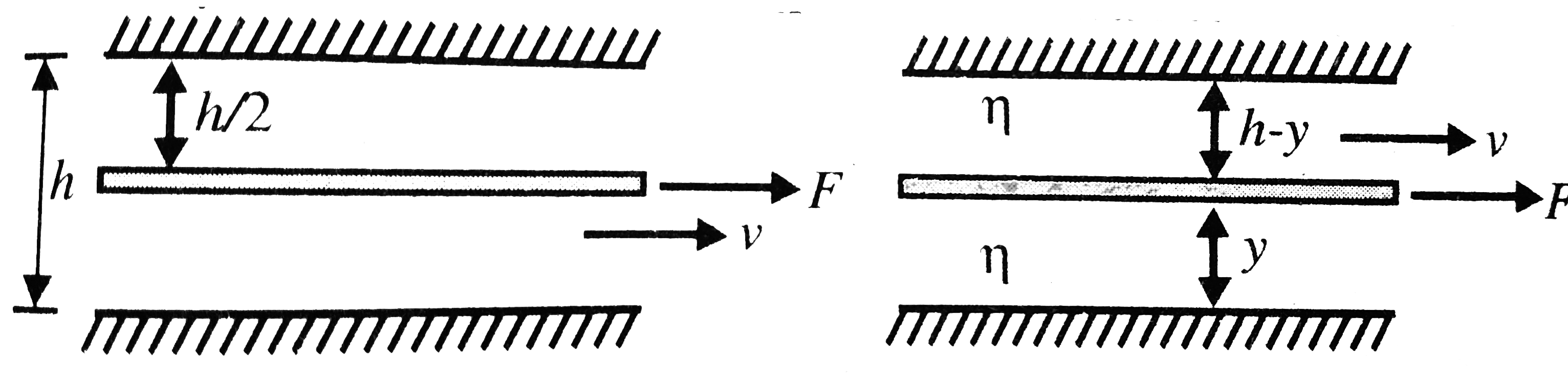
View Solution_S01_067_Q01.png)
A solid right cylinder of length l stands upright at rest on the bottom of a large tub filled with water up to height h as shown in the figure-I density of material of the cylinder equals to that of water. Now the cylinder is pulled slowly out of water with the help of a thin light inextensible thread as shown in figure-II. Find the work done by the tension force develop in the thread.
(a). mgh
(b). mgl
(c). 0.5 mgl
(d). mg(0.5l+h)
View SolutionMagnetic forces acting on conducting fluids provide a convenient means of pumping these fluids. For example, this method can be used to pump blood without damage to the cells that can be caused by a mechanical pump. A horizontal tube with rectangular cross section (height h, width W) is placed at right angles to a uniform magnetic field with magnitude B so that a length l is in the field (see figure). The tube is filled with conducting liquid and an electric current density J is maintained in the third mutually perpendicular direction.
Suppose the density of the liquid be ρ, then what would be the acceleration of liquid in the section abcd.

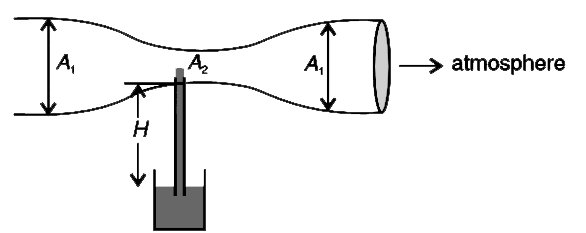
View Solution(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
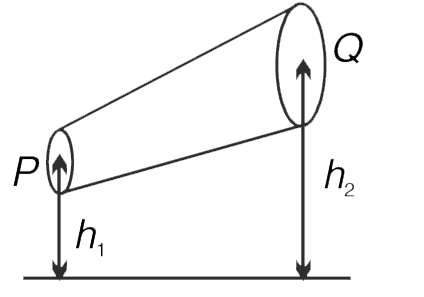
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View Solution(i) In the figure shown, the heavy cylinder (radius R) resting on a smooth surface separates two liquids of densities 2ρ and 3ρ. Find the height 'h' for the equilibrium of cylinder.
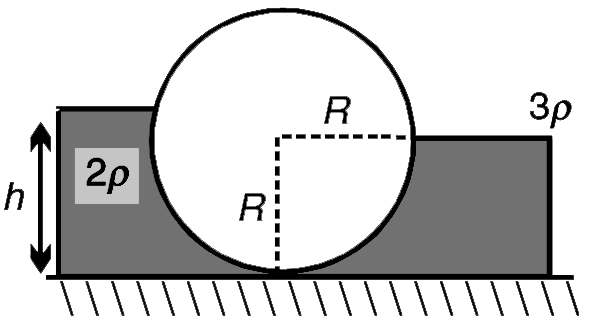
(ii) The cross section of a dam wall is an arc of a circle of radius R=20m subtending on angle of θ=60∘ at the centre of the circle. the centre (O) of the circle lies in the water surface. The width of the dam (i.e., dimension perpendicular to the figure) is b=10m. Neglect atmospheric pressure is following calculations.
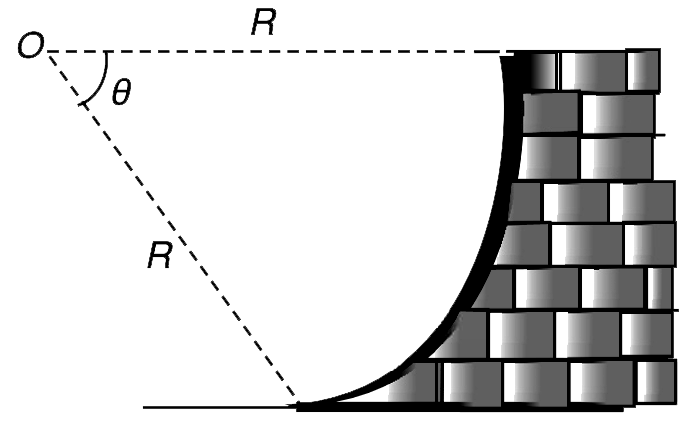
(a) Calculate the vertical component of force (Fx) applied by water on the curved dam wall.
(b) Calculate the horizontal component of force (FH) applied by water on the curved dam wall.
(c) Calculate the resultant force applied by the water on the curved dam wall.
View SolutionA thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity 0.75η0 at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity V. by applying the same force F? (Take h=20cm)

View Solution
