Two soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.
Excess pressure inside a soap bubble is 4T/r
IfP is the atmospheric pressure
P1=4Tr1=P, P2=4Tr2−P
∴P1−P2=4T(1r1−1r2)=4Tr12
∴1r12=1r1−1r2⇒r12=r1r2|r1−r2|
If r1>r2, P2>P1 and the intermediate film bulges towards the centre of circle of radius r1.

If r1=r2=2cm, the intermediate film is a plane symmetrical positioned. The 3 films due to the two bubbles and the intermediate film meet at a common circle with diameter AB. These 3 films produce 3 forces at every point of this circle.
Since the surface tension T is the same for all the films,
|F1|=|F2|=|F12|
Equilibrium at any point such as A is possible only if the three forces are at 120∘ to one antoher.
∴O1C=12r
b=r+12r=32r
Volume of each bubble before bursting =π3(32r)2(3t−32r)=9πr48
If R is the radius of the combined bubble after bursting the intermediate film,
4πR33=2×9πr38=9πr34


Topper's Solved these Questions
Similar Questions
Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View Solution
Knowledge Check
- Question 1 - Select One
Find the common radius of curvature when two soap bubbles with radii r1
Ar=r1+r22Br=r1+r2r1−r2Cr=r1r2r1+r2Dr=√r1r2 - Question 2 - Select One
The radii of two soap bubbles are R1 and R2 respectively. The ratio of masses of air in them will be
AR31R32BR32R31C⎛⎜⎝P+4TR1P+4TR2⎞⎟⎠R31R32D⎛⎜⎝P+4TR2P+4TR1⎞⎟⎠R32R31 - Question 3 - Select One
Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:
AinfiniteB2rCrDr/2
Two soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
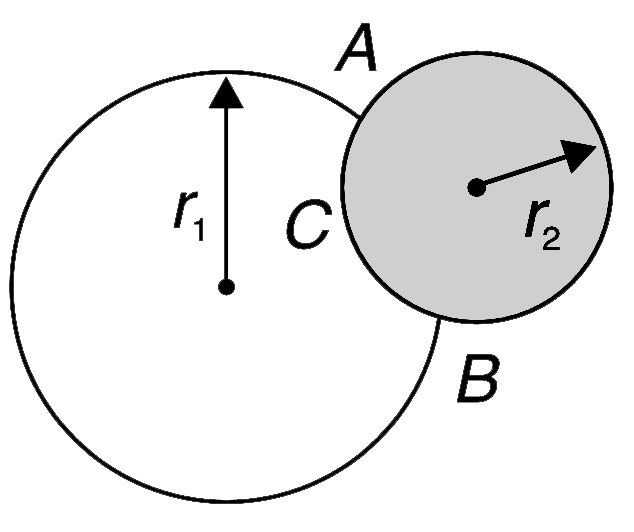 View Solution
View SolutionTwo soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionThe radii of two metallic spheres P and Q are r1 and r2, respectively. They are given the same charge. If r1>r2 then on connecting them with a thin wire, the charge will flow
View SolutionIf two soap bubbles of equal radii r coalesce then the radius of curvature of interface between two bubbles will be
View SolutionTwo soap bubbles coalesce.It noticed that, whilst joined together, the radii of the two bubbles are a and b where agtb.Then the radius of curvature of interface between the two bubbles will be
View Solution

