In the last problem if the scale for reading the height of mercury column is marked on the glass tube of the barometer, what reading will it show when temperature rises to θ2=35∘C ?
The correct Answer is:h=h0[1+γHgΔθ][1+αgΔθ]≅76.195cm
Step by step video, text & image solution for In the last problem if the scale for reading the height of mercury column is marked on the glass tube of the barometer, what reading will it show when temperature rises to theta_(2)=35^(@)C ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In design of a compensated pendulum, a light metal rod of length L0 = 1.0 m is attached to a glass tube filled with mercury. Neglecting the mass of the glass tube as well, calculate the height of mercury column in the glass tube so that centre of mass of this system does not rise or fall with temperature Given : λ)Hg)=1.82×10−4K−1,αglass')=9xx10^(-6),alpha_(mηl=1.2×10−5K−1
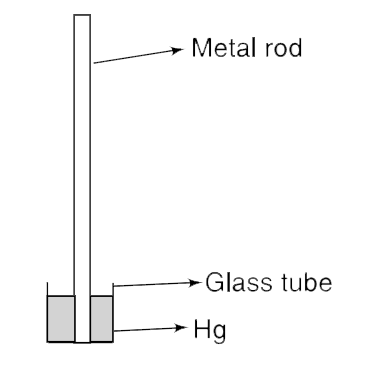
View SolutionHeight of mercury in a barometer is h0=76.0 cm at a temperature of θ1=20∘C. If the actual atmospheric pressure does not change, but the temperature of the air, and hence the temperature of the mercury and the tube rises to θ2=35∘C, what will be the height of mercury column in the barometer now? Coefficient of volume expansion of mercury and coefficient of linear expansion of glass are
γHg=1.8×10−4.∘C−1,αg=0.09×10−4.∘C−1
View Solution
Knowledge Check
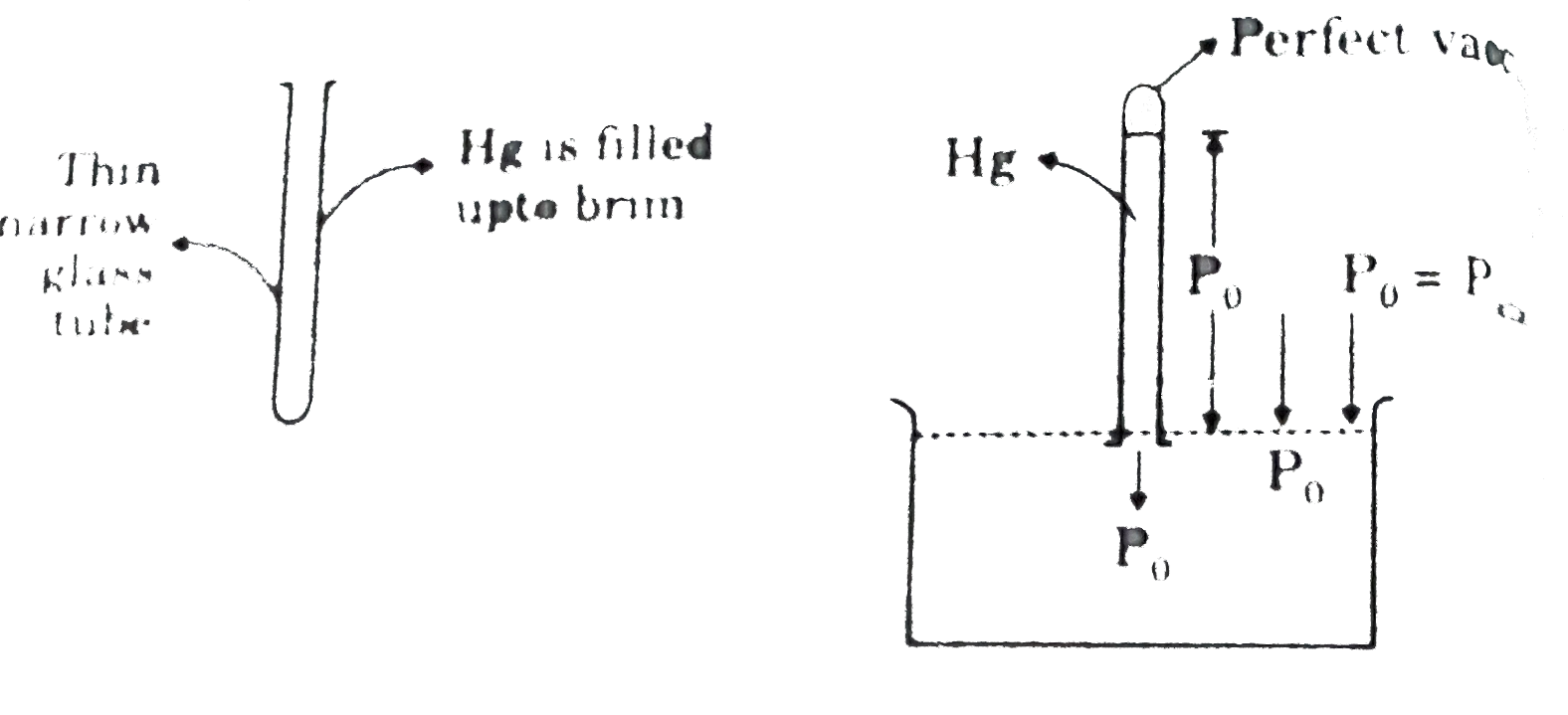
A barometer is an instrument that is used for the measurement of pressure The construction of the barometer is as follows:
A thin narrow calibrated capillary tube is filled to the brim with a liquid such as mercury and is inverted into a through filled with the same fluid Now depending on the external atmospheric pressure the level of the inside capillary comes to rest, then the net forces on the column should be balanced Applying force balance we get Patm×A=m×g
(A is the cross-sectional area of the capillary tube) if ρ is the density of the fluid, then m=ρ×g×h
(h is the height to which mercury has risen in the capillary)
Hence Patm×A=(ρ×g×h)×AorPatm=ρgh
Faulty Barometer:
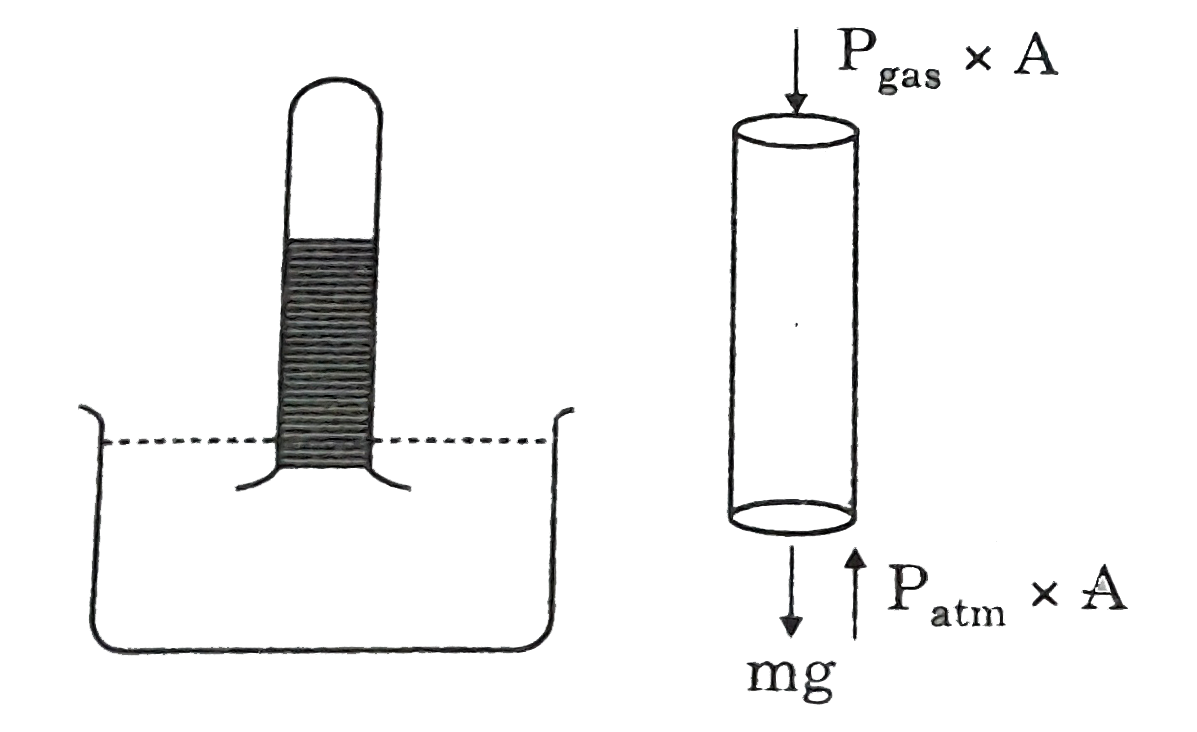
An ideal barometer will show a correct reading only if the space above the mercury column is vacuum but in case if some gas column is trapped in the space above the mercury column then the barometer is classified as a faulty barometer. The reading of such a barometer will be less than the true pressure
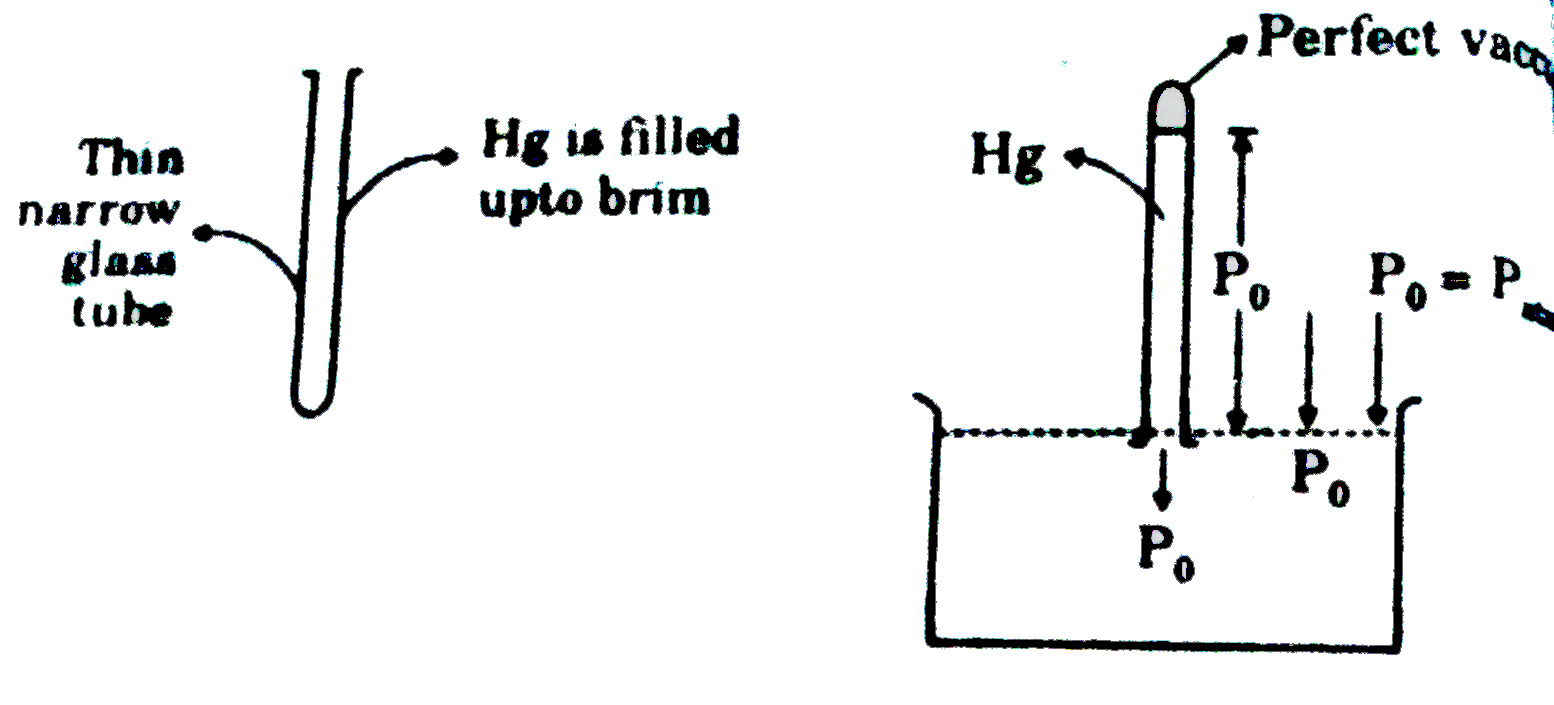
For such a faulty barometer
P0A=mg+PgasA
P0=ρhg+Pgas
or ρgh=P0−Pgas
A tube closed at one end is dipped in mercury as shown in figure such that the closed surface coincides with the mercury level in the container By how much length of the tube should be extended such that the level of Hg in the tube is 5 cm below the mercury level inside the container? (Assume temperature remains constant)
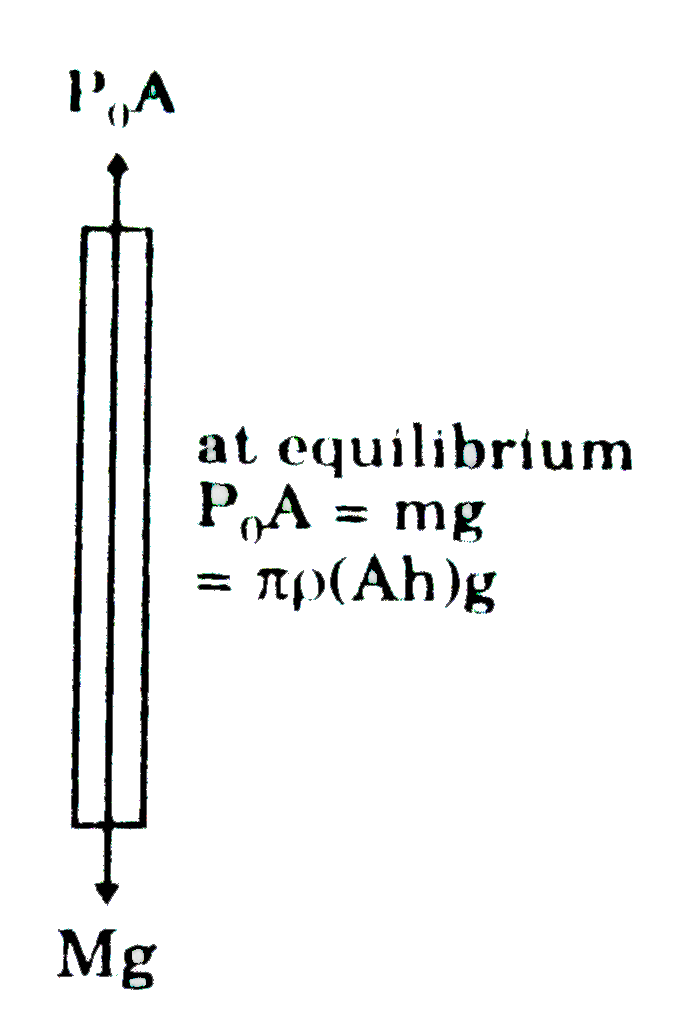

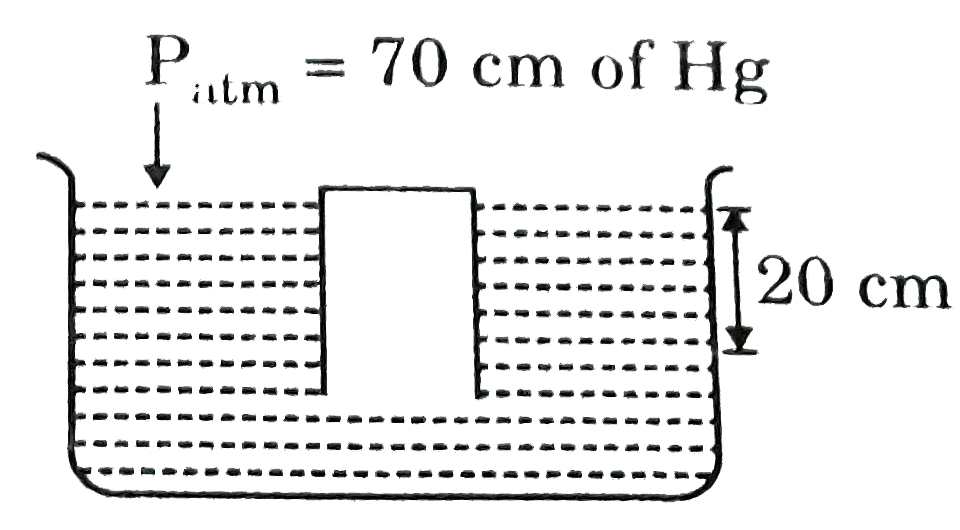 A18 cmB19 cmC24 cmD30 cm
A18 cmB19 cmC24 cmD30 cmA barometer is an instrument that is used for the measurement of pressure The construction of the barometer is as follows:
A thin narrow calibrated capillary tube is filled to the brim with a liquid such as mercury and is inverted into a through filled with the same fluid Now depending on the external atmospheric pressure the level of the inside capillary comes to rest, then the net forces on the column should be balanced Applying force balance we get Patm×A=m×g
(A is the cross-sectional area of the capillary tube) if ρ is the density of the fluid, then m=ρ×g×h
(h is the height to which mercury has risen in the capillary)
Hence Patm×A=(ρ×g×h)×AorPatm=ρgh
Faulty Barometer:
An ideal barometer will show a correct reading only if the space above the mercury column is vacuum but in case if some gas column is trapped in the space above the mercury column then the barometer is classified as a faulty barometer. The reading of such a barometer will be less than the true pressure
For such a faulty barometer
P0A=mg+PgasA
P0=ρhg+Pgas
or ρgh=P0−Pgas
If the tube shown below is placed vertically with the open and upward then the length of the air column will be (Assume temperature remains constant)

 A20 cmB36 cmC18 cmD15 cm
A20 cmB36 cmC18 cmD15 cmA student is performing the experiment of Resonance Column. The diameter of the column tube is 4cm. The diameter of the column tube is 4cm. The frequency of the tuning fork is 512Hz. The air temperature is 38∘C in which the speed of sound is 336m/s. The zero of the meter scale coincides with the top end of the Resonance column tube. When the first resonance occurs, the reading of the water level in the column is
A14.0cmB15.2cmC16.4cmD17.6cm
A barometer tube contains a mixture of air and saturated water vopour in the space above the mercury column. It reads 70cm when the actual atmospheric pressure is 76cm of mercury. The saturation vapour pressure at roon tempature is1.0 cm of mercury, The tube is now lowered in the reservoir till the space above the mercury cloumn is reduced to half its origina volume. Find the reading of the barometer. Assume that the temperature remains constant.
View SolutionA berometer correctlu reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric tgemperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionWhen the mercury thread rises to 3/4th of the distance between the two fixed points, what is the temperature indicated by the Fahrenheit scale?
View SolutionA tube 2m long and closed at on e end is half filled with mercury and is then inverted with its open end just dipping into a mercury trogy. Find the height of mercury which will stand in the tube if the reading of the barometer is o.75 m.
[hint: P1=0.765,V1=1∝m3,P2=(3/4−x),V2=(2−x)∝m3,usep1V2=P2V2.]
View SolutionThe reading of a barometer containing some air above the mercury column is 73cm while that of a correct one is 76cm. If the tube of the faulty barometer is pushed down into mercury until volume of air in it is reduced to half, the reading shown by it will be:
View Solution
