Two square metal plates have sides of length L and thickness $t (< < < L)$ . They are arranged parallel to each other with their inner faces at a separation of $\frac{5}{2}$ t. One of the plates is given a charge $- Q$ and the other one is given a charge $+ Q$ . A third rectangular metal plate of sides L and x, having thickness $\frac{t}{2}$ is inserted between the plates as shown. The third plate is equidistant from the two plates and parallel to them. Neglect edge effects.

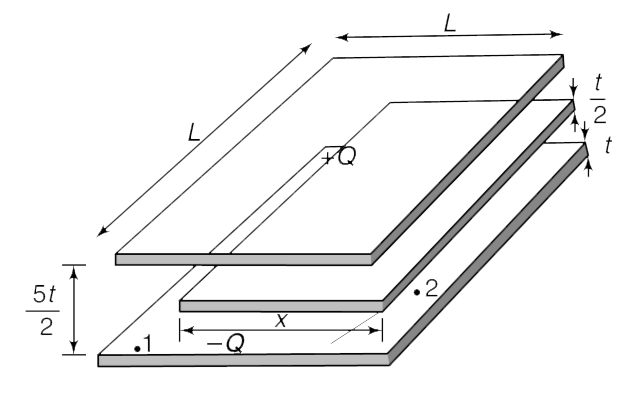
(a) Find the charge density on lower plate at points 1 and 2 shown in Figure.
(b) Find potential difference between the upper plate and the middle plate.
(c) Find electric field between the two outer plates in space where the third plate is not present (i.e., at a point above point 1.)
(d) Find the capacitance of the system across two outer plates.

Text Solution

Verified by Experts

The correct Answer is:(a) $σ_{1} = \frac{4 Q}{L (4 L + x)}; σ_{2} = \frac{5 Q}{L (4 L + x)}$
(b) $\frac{5 Q t}{\in_{0} L (4 L + x)}$
(c) $\frac{4 Q}{\in L (4 L + x)}$
(d) $\frac{\in_{0} L (4 L + x)}{10 t}$

Updated on:21/07/2023

Each of two large conducting parallel plates has one sided surface area A. If one of the plates is given a charge Q whereas the other is neutral, then the electric field at a point in between the plates is given by
A $\frac{Q}{A ε_{0}}$
B $\frac{Q}{2 A ε_{0}}$
C $\frac{Q}{4 A ε_{0}}$
DZero
A metallic plate of thickness (t) and face area of one side (A) is inserted between the plates of a parallel plate air capacitor with a separation (d) and face are (A). Then the equivalent capacitance is
A $\frac{\in_{0} A}{d}$
B $\frac{\in_{0} A}{(d \cdot t)}$
C $\frac{\in_{A}}{(d - t)}$
D $\frac{\in_{0} A}{(d + t)}$
Separation between the plates of a parallel plate capacitor is $d$ and the area of each plates is $A$ . When a slab of material of dielectric constant $k$ and thickness $t (t < d)$ is introduced between the plates. Its capacitance becomes
A $\frac{ε_{0} A}{d + t (1 - \frac{1}{k})}$
B $\frac{ε_{0} A}{d + t (1 + \frac{1}{k})}$
C $\frac{ε_{0} A}{d - t (1 - \frac{1}{k})}$
D $\frac{ε_{0} A}{d - t (1 + \frac{1}{k})}$