A non-conducting disc of radius a and uniform positive surface charge density $σ$ is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc, from a height H with zero initial velocity. The particle has $q / m = 4 \in_{0} g / σ$
(a) Find the value of H if the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(i) $H = \frac{4}{3} a$ (ii) $H = \frac{a}{\sqrt{3}}$

Potential at a height H on the axis of the disc V(P):
The charge dq contained in the ring shown in figure.
Potential of p due to this ring

$d V = \frac{1}{4 π ε_{0}} . \frac{d q}{x}$ where $x = \sqrt{H^{2} + r^{2}}$
$d V = \frac{1}{4 π ε_{0}} . \frac{(2 π r d r) σ}{\sqrt{H^{2} + r^{2}}} = (\frac{σ}{2 ε_{0}}) \times (\frac{r d r}{\sqrt{H^{2} + r^{2}}})$
$∴$ Potential due to the complete disc
$V_{p} = r = a \int r = 0 d V = \frac{σ}{2 ε_{0}} r = a \int r = 0 \frac{r d r}{\sqrt{H^{2} + r^{2}}}$
$V_{p} = \frac{σ}{2 ε_{0}} [\sqrt{a^{2} + H^{2}} - H]$
Potential at centre (O) will be $V_{O} = \frac{σ a}{2 ε_{0}} ∴ H = 0$
(i) Particle is released from P and just reaches point O. Therefore from conservation of mechanical energy.
Decrease in graviational potential energy
= Increase in electrostatic potential energy
$(Δ K E = 0$ because $K_{1} = K_{f} = 0$ )
$∴ m g h = q [V_{o} - V_{p}] \Rightarrow g H = (\frac{q}{m}) (\frac{σ}{2 ε_{0}})$
$[a - \sqrt{a^{2} + H^{2}} + H]$ ...(i)
$\frac{q}{m} = \frac{4 ε_{0} g}{σ} ∴ \frac{q σ}{2 ε_{0} m} = 2 g$
Substituting in Eq. (i), we get
$g H = 2 g [a + H - \sqrt{a^{2} + H^{2}}]$
$\Rightarrow \frac{H}{2} = (a + H) - \sqrt{a^{2} + H^{2}}$
$\Rightarrow \sqrt{a^{2} + H^{2}} = a + \frac{H}{2}$
$\Rightarrow a^{2} + H^{2} = a^{2} + \frac{H^{2}}{4} + a H \Rightarrow \frac{3}{4} H^{2} = a H$
$\Rightarrow H = \frac{4}{3} a$ and $H = 0 ∴ H = (\frac{4}{3}) a$
(ii) Potential energy of the particle at height H=Electrostatic potential energy + gravitational potential energy
$∴ U = q V + m g H$
Here V=Potential at height H
$U = \frac{σ q}{2 ε_{0}} [\sqrt{a^{2} + H^{2}} - H] + m g H$ ...(ii)
At equilibrium position $F = \frac{- d U}{d H} = 0$
Differentialting Eq. (ii) w.r.t H
$\Rightarrow m g + σ \frac{q}{2 ε_{0}} [(\frac{1}{2}) (2 H) \frac{1}{\sqrt{a^{2} + H^{2}}} - 1] = 0$
$(∵ \frac{σ q}{2 ε_{0}} = 2 m g)$
$∴ m g + 2 m g [\frac{H}{\sqrt{a^{2} + H^{2}}} - 1] = 0$
$\Rightarrow 1 + \frac{2 H}{\sqrt{a^{2} + H^{2}}} - 2 = 0 \Rightarrow \frac{2 H}{\sqrt{a^{2} + H^{2}}} = 1$
$\Rightarrow \frac{H^{2}}{a^{2} + H^{2}} = \frac{1}{4} \Rightarrow 3 H^{2} = a^{\circ} \Rightarrow H = \frac{a}{\sqrt{3}}$
From Eq. (ii) we can write U-H equation as
$U = m g (2 \sqrt{a^{2} + H^{2}} - H)$
(Parabolic variation)
$U = 2 m g a$ at $H = 0$
and $U = U_{min} = \sqrt{3} m g a$ at $H = \frac{a}{\sqrt{3}}$
therefore, $U - H$ graph will be as shown.

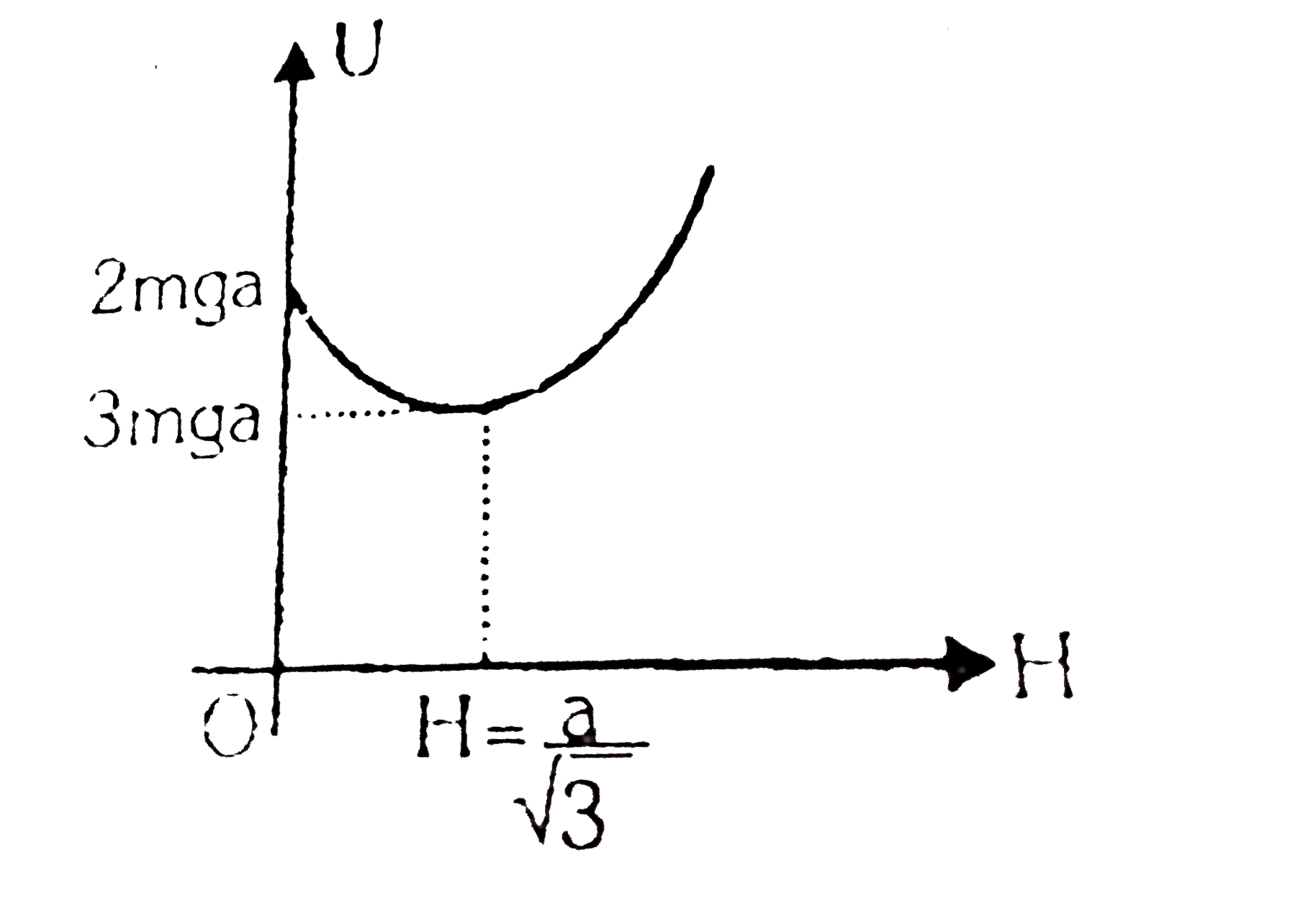
Note that at $H = \frac{a}{\sqrt{3}}$ , U is minimum.
Therefore, $H = \frac{a}{\sqrt{3}}$ is stable equilibrium position.

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
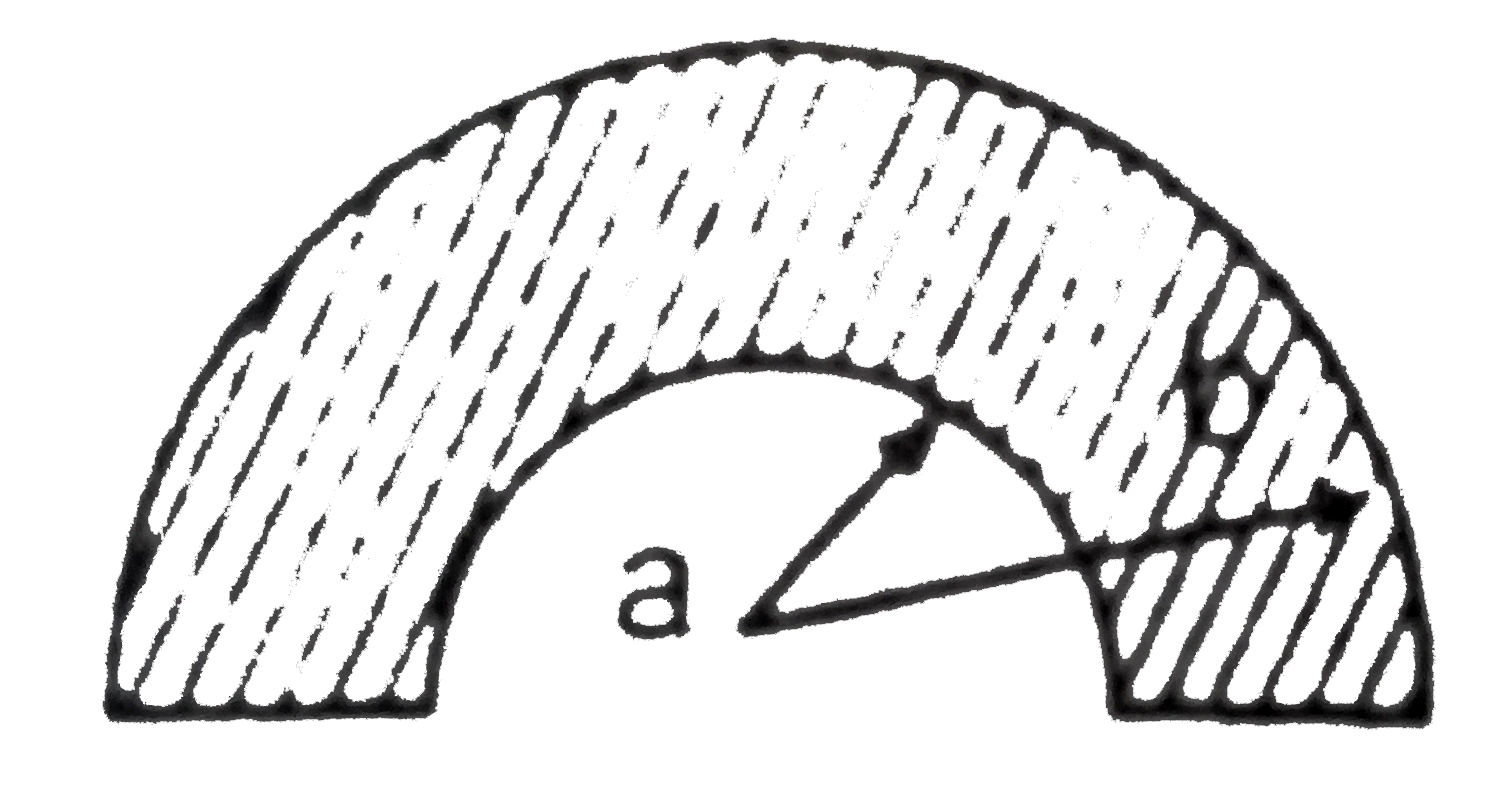
A non-conducting semi circular disc (as shown in figure) has a uniform surface charge density $σ$ . The ratio of electric field to electric potential at the centre of the disc will be

A $\frac{1}{π} \frac{ln b / a}{(b - a)}$
B $\frac{2}{π}$
C $\frac{1}{π} \frac{{ln (b / a)}^{2}}{(b - a)}$
D $\frac{π (b - a)}{2 ln (b / a)}$

ALLEN-MISCELLANEOUS-SUBJECTIVE QUESTION

Home
Ask Doubt
Profile