Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.
The correct Answer is:(v0)min=3m/s,K=3×10−4J
In the figure
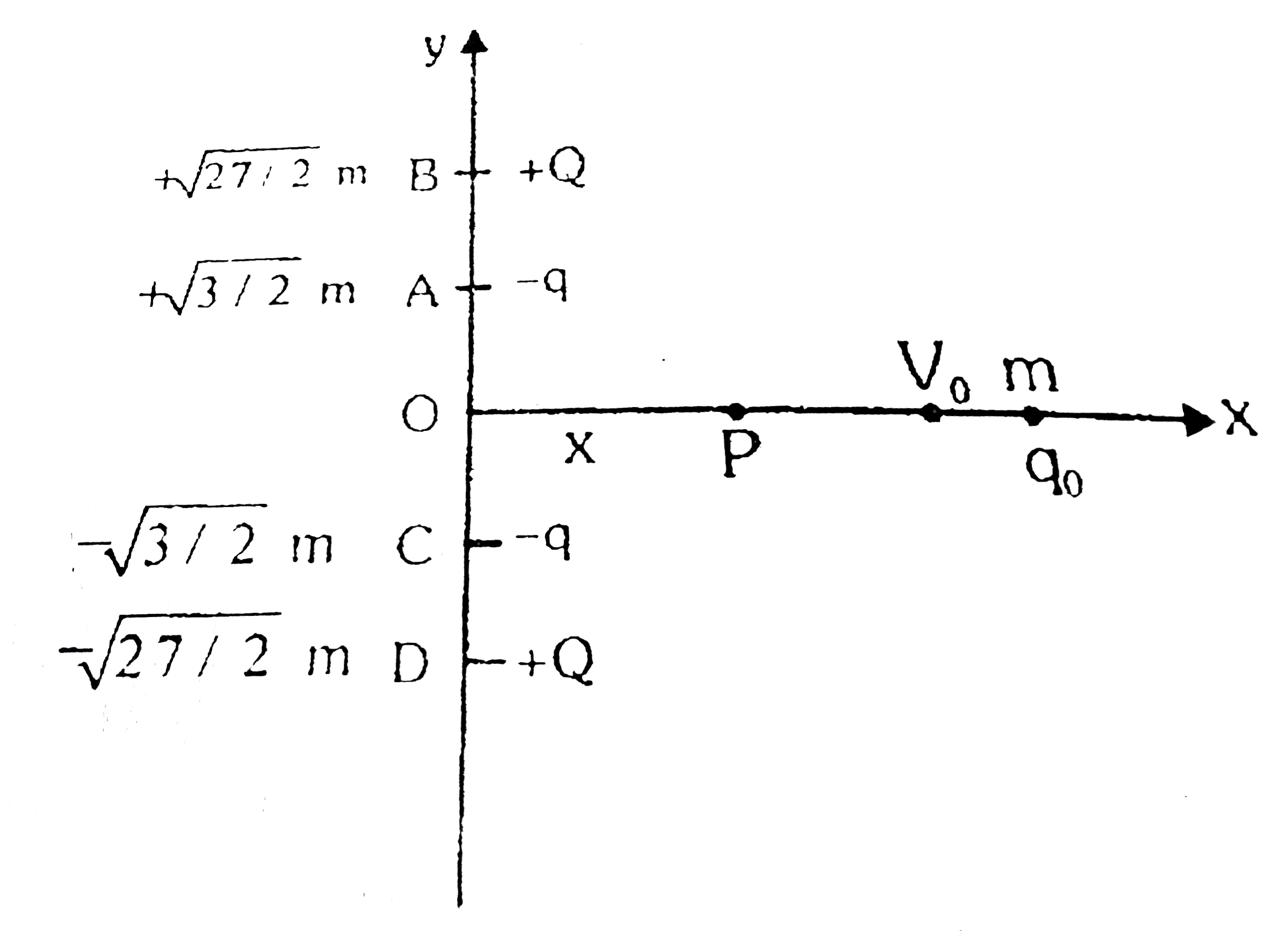
q=1μC=10−6C,q0=+0.1μC=10−7C
and
m=6×10−4kg and Q=8μC=810−6C
Let P be any point at a distance x from origin O. Then
AP=CP=√32+x2
BP=DP=√272+x2
Electric potential at point P will be
V=2KQBP−2KqAP
where K=14πε0=9×109N/m2/C2
∴V=2×9×109⎡⎢
⎢⎣8×10−6√272+x2−10−6√32+x2⎤⎥
⎥⎦
V=1.8×104⎡⎢
⎢⎣8√272+x2−1√32+x2⎤⎥
⎥⎦ ...(i)
∴ Electric field at P is
E=−dVdx=1.8×104
⎡⎣(8)(−12)(272+x2)−32−(−12)(32+x2)−32⎤⎦(2x)
E=0 on x-axis where −x=0 or
8(272+x2)3/2=1(32+x2)3/2
⇒(4)3/2(272+x2)3/2=1(32+x2)3/2
⇒(272+x2)=4(32+x2)
This equation gives x=±√52m
The least value of kinetic energy of the particle at infinity should be enough to take particle upto
x=+√52m because at x=+√52m,E=0
⇒ Electrotatic force on charge q is zero or Fe=0. For at x>√52m, E is repulsive (towards x-axis) and for x<√52m, E is attractive (towards negative x-axis).
Now, from Eq. (i) potential at x=√52m
v=1.8×104⎡⎢
⎢⎣8√272+52−1√32+52⎤⎥
⎥⎦
⇒V=2.7×104 volt
Applying energy conservation at x=∞ and x=√52m,12mv20=q0V ...(ii)
∴v0=√2q0Vm
Substituting the values
v0=√2×10−7×2.7×1046×10−4⇒v0=3m/s
∴ Minimum value of v0 is 3m/s
From eq. (i) potential at origin (x=0) is
V0=1.8×104⎡⎢
⎢⎣8√272−1√32⎤⎥
⎥⎦≈2.4×104V
Let K be the kinetic energy of the particle at origin. Applying energy conservation at x=0 and x=∞
K+q0V0=12mv20 But 12mv20=q0V [from Eq. (ii)]
K=q0(V−V0)=(10−7)(2.7×104−2.4×104)
⇒K=3×10−4J
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - LINKED COMPREHENSION TYPE3videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Four point charges +8mC, −mC, and +8mC are fixed at the points −√272m, −√32m, +sqrt(3/2)mand+sqrt(27/2)mrespectivelyonthey−aξs.Apartic≤ofmass6xx10^-4kgandchar≥+0.1muCmovesalongthe−xdirection.Itsspeedatx=+ooisV_0.F∈dthe≤∗valueofV_0forwhichthepartic≤willcrosstheorig∈.F∈dalsothek∈etice≠rgyofthepartic≤attheorig∈.As∑etˆspaceisgravityee.<br>Given(1)/(4piepsilon_0)=9xx10^9Nm^2//C^2.
View SolutionFour point +8μC,−1μC,−1μC, and +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m, and +√27/2m, respectively, on the y - axis. A particle of mass 6×10−4kg and charge +0.1μC moves along the x- direction. Its speed at x=+∞ is V0. Find the least value of V0 for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. Given (1/4πε0)=9×109Nm2C−2.
View Solution
Knowledge Check
- Question 1 - Select One
Four point charges q, -2q, -q and 2q are placed at points (0,0,0) m , (√2,0,0)m,(√2,√2,0)m and (0,√2,0) m respectively . The electric field at point (1√2,1√2,0)m is (q=1μC)
A18×103N/CB36×103N/CC18√5×103N/CD18√3×103N/C - Question 2 - Select One
Three point charges 1μC,1μC and −2μC are placed at points having coordinates (0,1,0)cm, (1,0,0) cm and (0,0,0)cm respectively. The magnitude of electric dipole moment of the system is
A10−8CmB√2×10−8CmC√3×10−8CmD2×10−8Cm - Question 3 - Select One
Electric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
A1.8 VB1.8×106VC1.8×105VD1.8×104V
Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
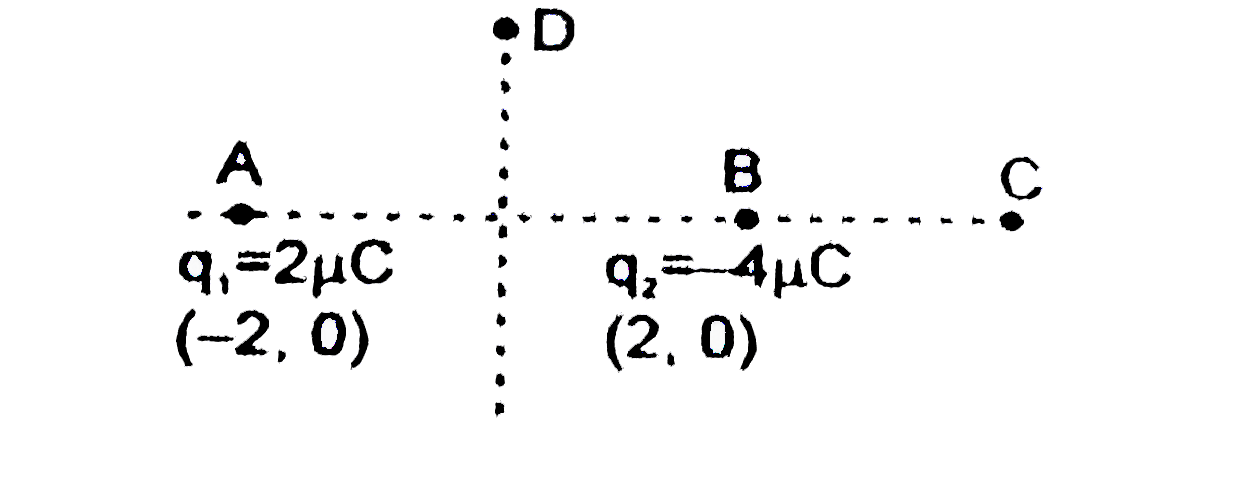 View Solution
View SolutionTwo point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionA particle of mass m=5kg is moving with a uniform speed v=3√2 in the XOY plane along the line Y=X+4. The magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m = 5 units is moving with a uniform speed v=3√2 units in the XOY plane along the line Y = X + 4. The magnitude of the angular momentum of the particle about the origin is
View Solution

