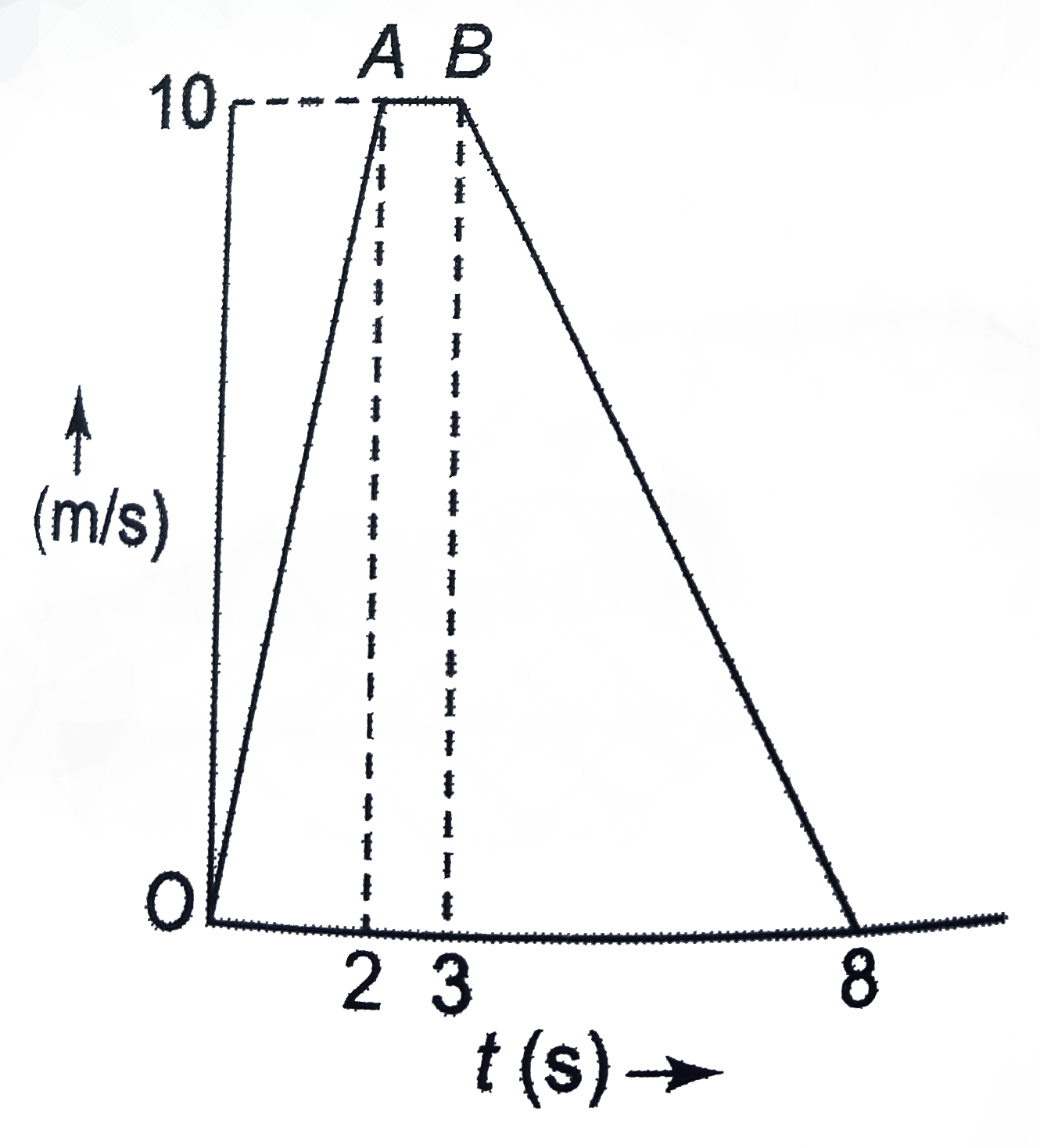
Acceleration of particle moving in straight line can be written as . From the given graph find acceleration at .

The correct Answer is:
From graph
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-4[B]
Explore 14 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:EXERCISE-5(A)
Explore 15 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:DATA SUFFICIENCY QUESTIONS
Explore 3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
For a particle moving in a straight line, the velocity-time graph is as shown in the figure. Find the acceleration at time t=1s2.5s and 5s. Sketch the acceleration time graph.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View Solution
Knowledge Check
Let v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
A|a|Bv.avCthe component of a parallel to vDthe component of a perpendicular to vFor a particle moving in straight line with increasing speed the sppropriate sign of acceleration a and velocity v can be:
Aa>0 and v>0Ba<0 and v<0Ca>0 and v<0Da<0 and v>0The speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
AxbBxabCabxDax
Acceleration of two identical particles moving in a straight line are as shown in figure.

The corresponding a-t graph of their centre of mass will be
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View SolutionThe velocity of a particle moving in straight line is given by the graph shown here. Then its acceleration is best represented by :
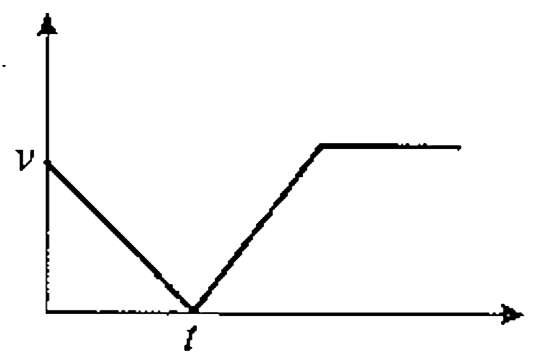
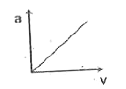
View SolutionAcceleration-velocity graph of a particle moving in a straight line is as shown in the figure. Then slope of velocity-displacement graph
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
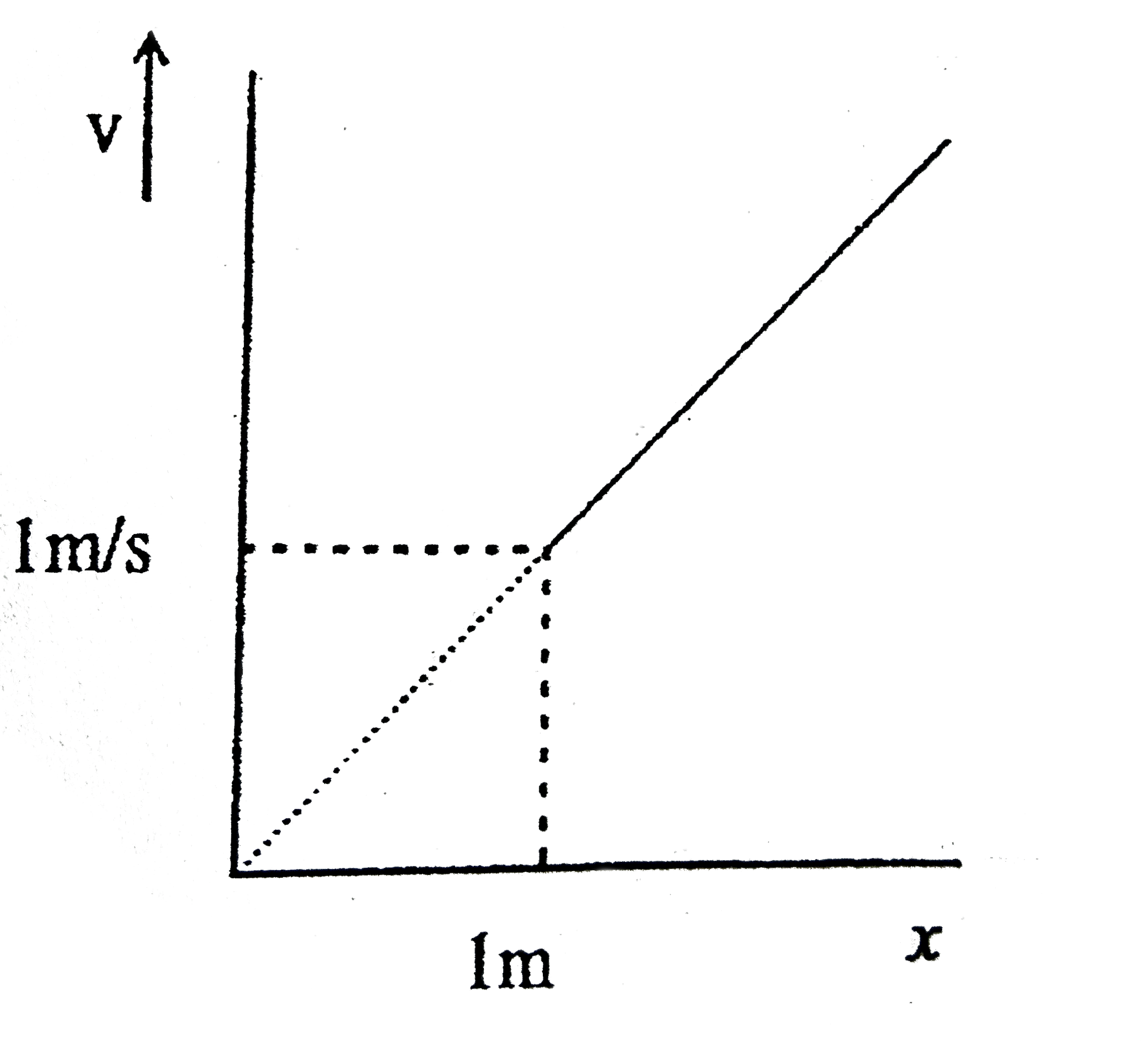
View Solution