An infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released from point P on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the plane of the sheet.
.
The correct Answer is:v=√σeRm∈0
From energy conservation
[σR2∈0−σ2∈0×2R]e=−12mv2
−σRe2∈0+σRe∈0=12mv2
v=√σeRm∈0
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)35videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)19videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[A]34videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
An infinite dielectric sheet having charge density σ has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the plane of the sheet.
. View SolutionAn infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.
View Solution
Knowledge Check
- Question 1 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
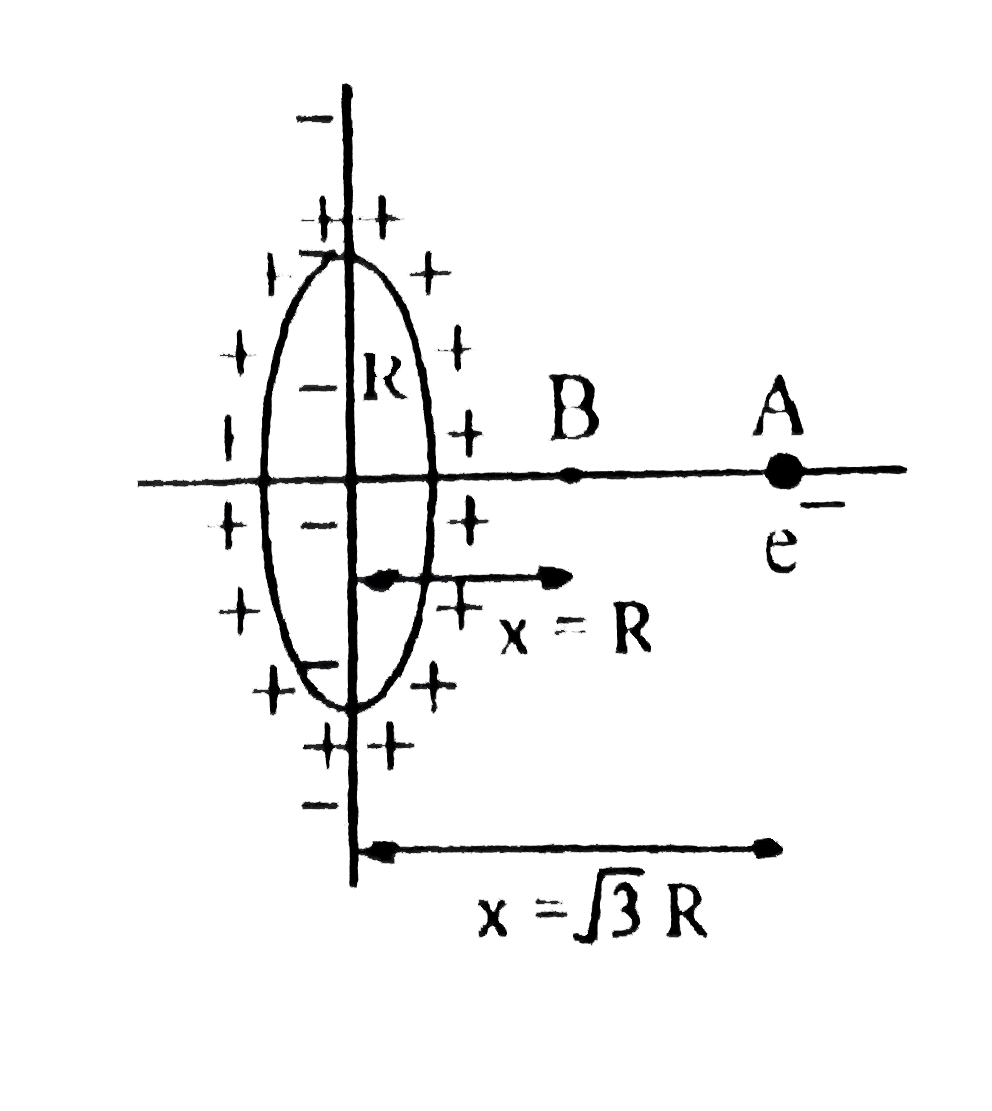
Magnitude of initial acceleration of the electron.Aeλπɛ0mR(3−2√24√6)Beλπɛ0mR(3+2√24√6)Ceλπɛ0mR(3+2√24√3)Dnone - Question 2 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
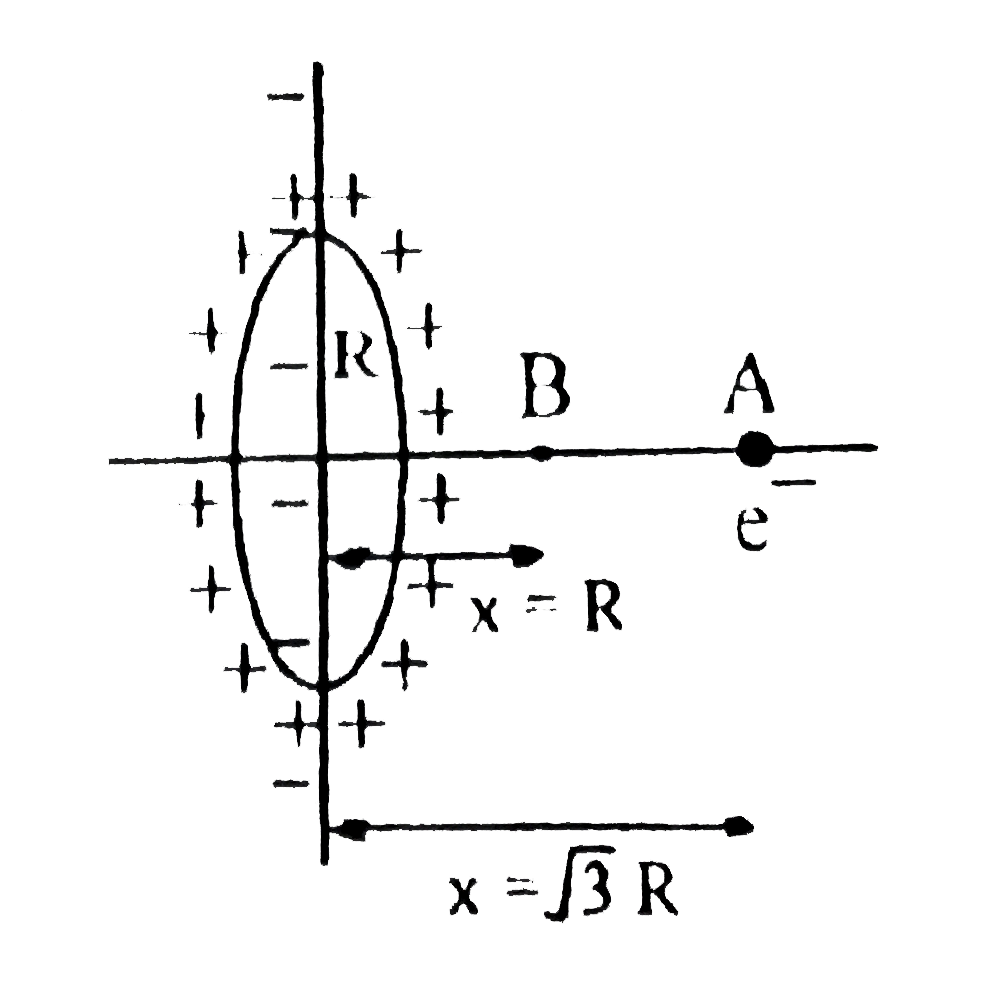
The distance from centre of ring on the axis where the net force on the electron is zero.A2RB√2RCRDnone of these - Question 3 - Select One
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
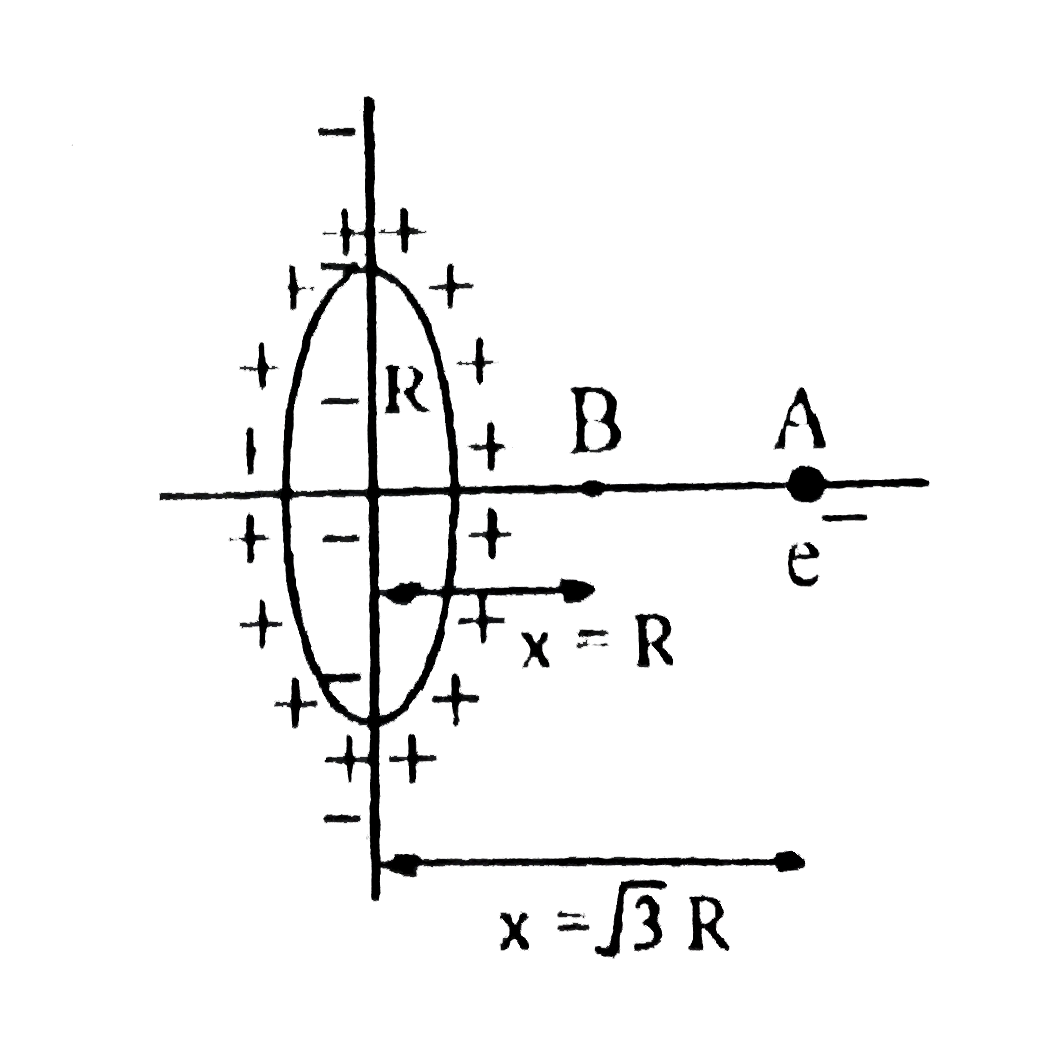
Potential difference between points A(x=√3R) and B(x=R)i.e.(VA−VB) isA−λπɛ0[(1−1√2)−ln34]B−λπɛ0[(1−1√2)−ln34]C−λπɛ0[(1+1√2)−ln34]Dnone
A large metallic plate is facing a charged sheet having charge density σ placed parallel to plate at a distance l from the plate.Potential at point P at a distance x from the sheet is
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
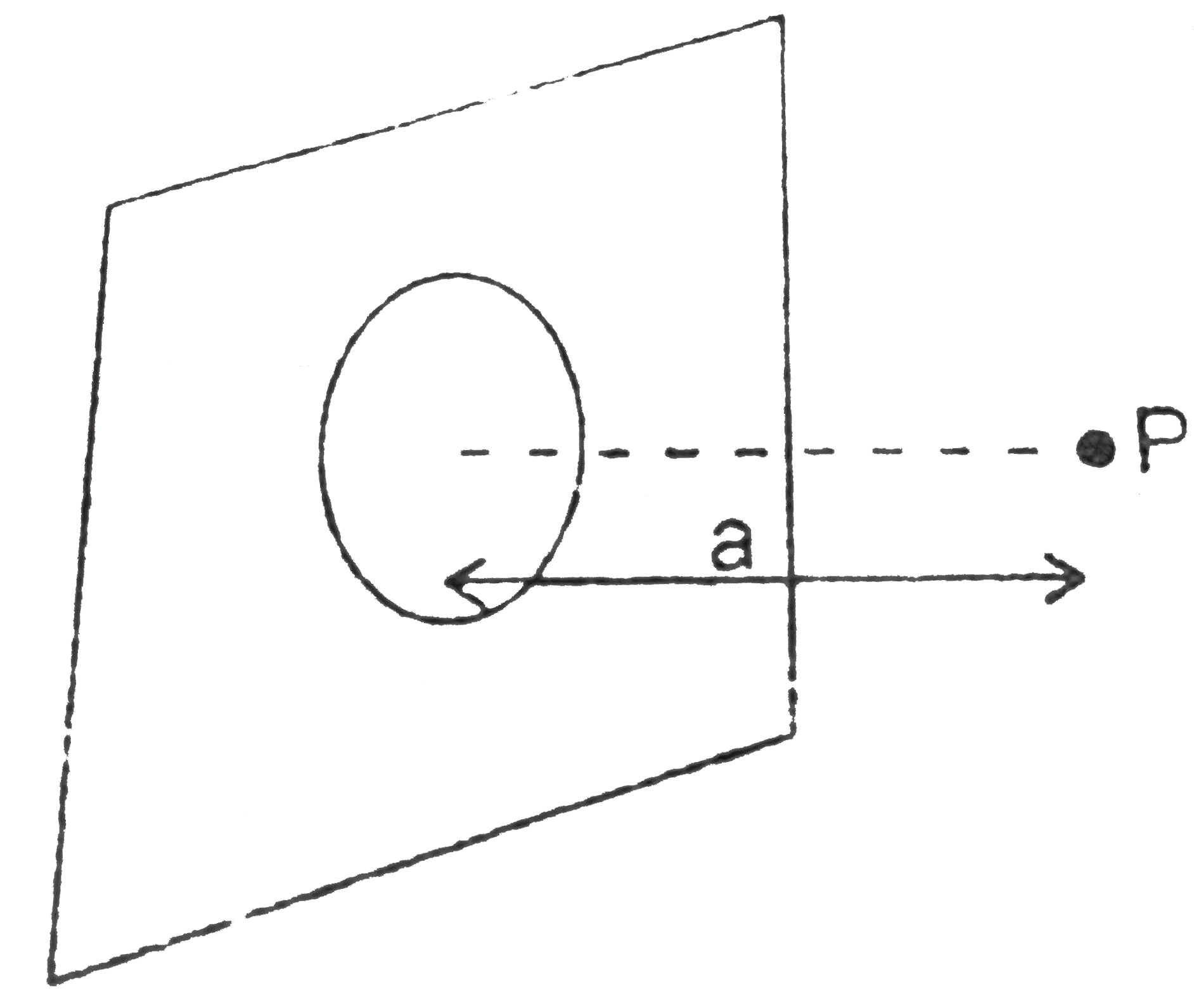View SolutionA large metallic plate is facing a charged sheet having charge density "sigma" placed parallel to plate at a distance "l" from the plate.Potential at "point "P" at a distance [x" from the sheet is "]
View SolutionThin infinite sheet of width w contains uniform charge distribution σ. Find out electric field intensity at following points :
(a) A point which lies in the same plane at a distance d from one of its edge.
(b) A point which is on the symmetry plane of sheet at a perpendicular distance d from it.
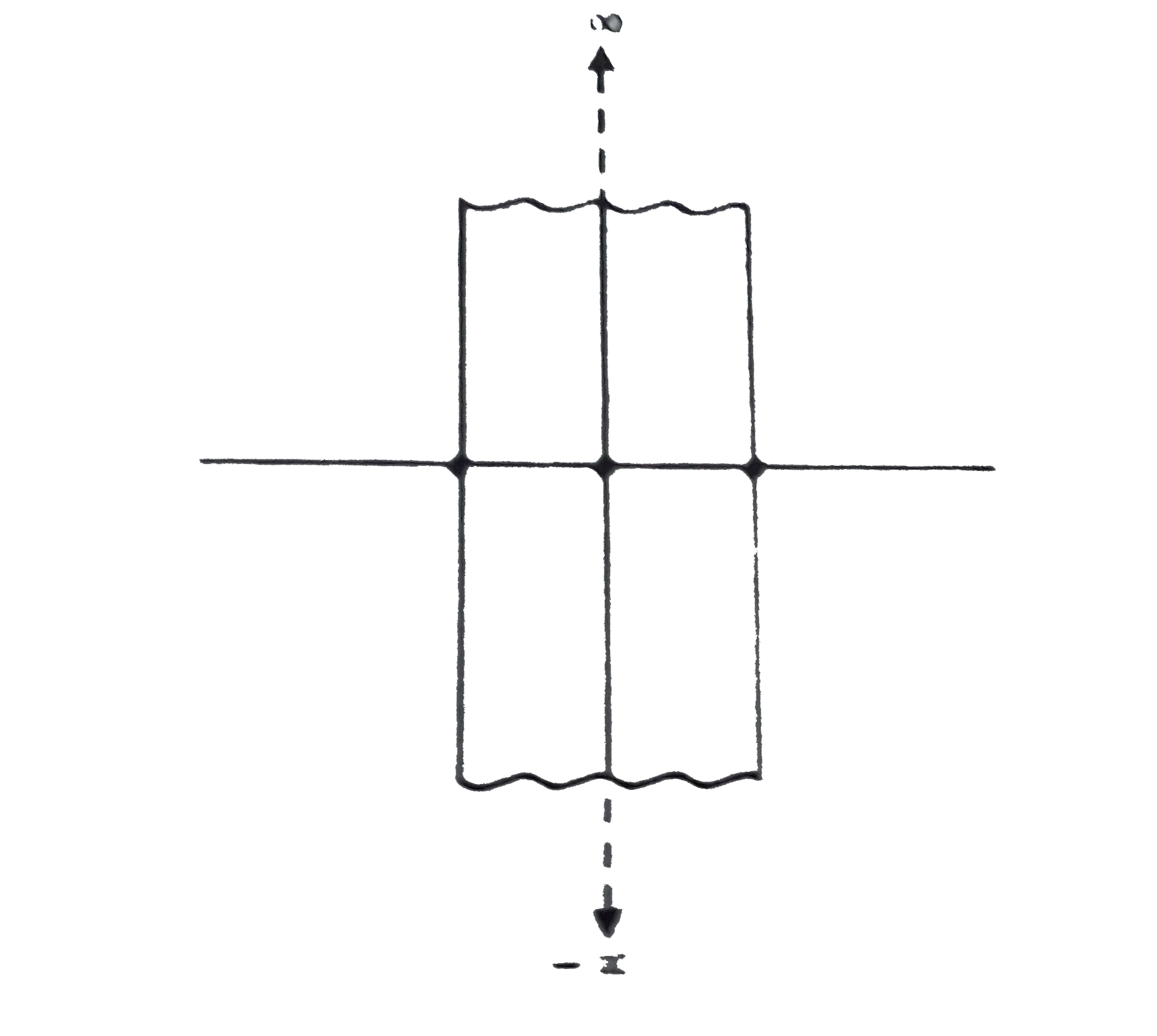View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
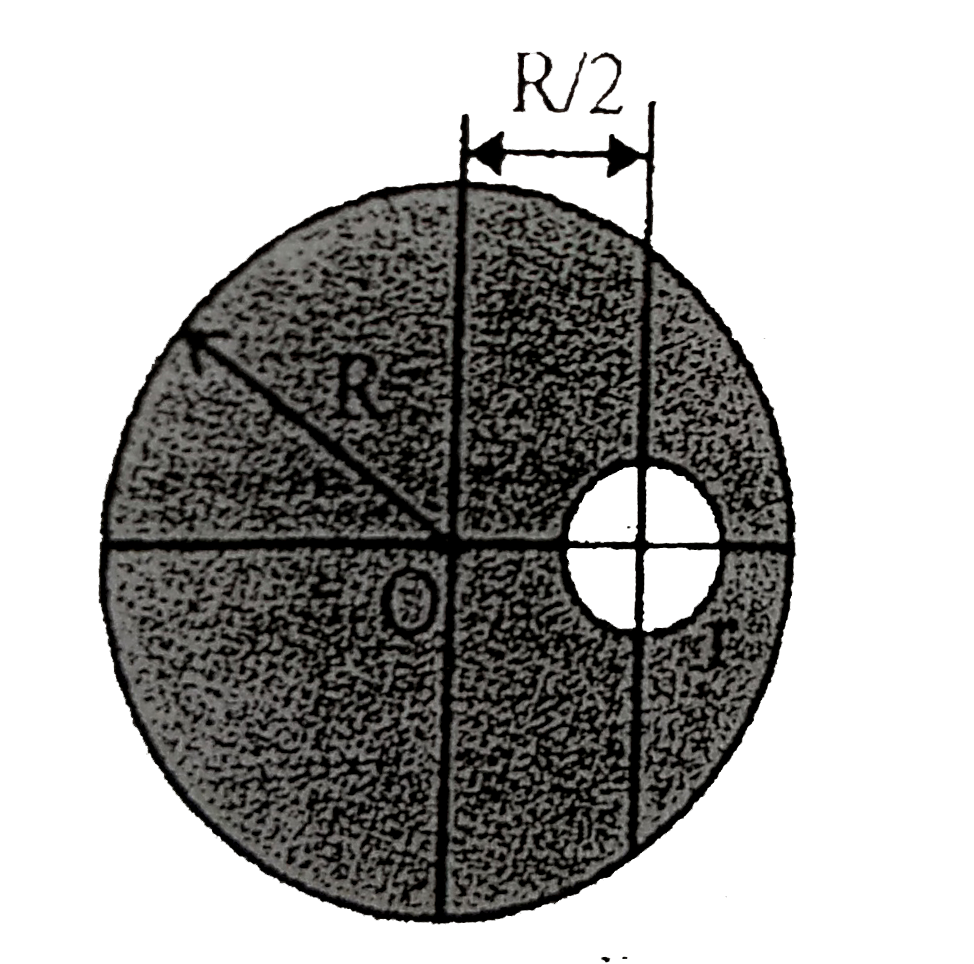View Solution