Figure shown a section through two long thin concentric cylinders of radii a & b with a>b. The cylinders have equal and opposite per unit length λ. Find the electric field at a distance r from the axis for (i) r<a (ii) a<r<b (iii) r>b

[i] r<a⇒ Point inside ⇒E=0
[ii] a<r<b⇒ Point outside the inner and inside the outer so field due to only inner cylinder
hence E=2×λr
[iii] r>b⇒ point outside from both cylinders so the charge per unit length (λ) is zero point (r>b)∴E=0
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)35videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)19videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[A]34videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
A cylinder space of radius R is filled with a unifrom magnetic induction a parallel to the axis of the space . If B change at the rate .Find the electric field at a distance (i) r<R (ii) r>R
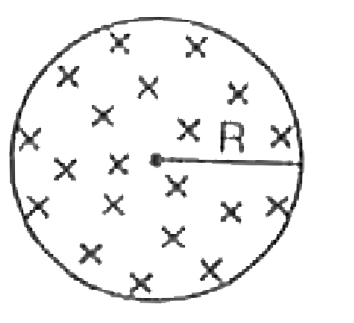 View Solution
View SolutionConsider a system of two long coaxial cylinders: solid (of radius a carrying i current in positive z direction) and hollow (or radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from of the cylinders for
(i) r≤a
(ii) a<r<b
(iii) r>b
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The electric field at a distance r from a long wire having charge per unit length λ is
AE=2πε0λKr2BE=ε0λ2πKr2CE=λ2πε0KrDE=4πε0λKr2 - Question 2 - Select One
The electric field at a distance r from a long wire having charge per unit length λ is
Ak(λr2)Bk(λr)Ck(λ2r)Dk(2λr)
The adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
 View Solution
View SolutionA uniform magnetic field exists in a circular region of radius R centrad at O. The field is perpendicular to the plane of paper and is strength varies with time as B=B0t. Find the induced electric field at a distance r from the centre for (i)r<R, (ii) r>R. Also, plot a graph between |E| and r for both the cases.
View SolutionTwo thin cocentric and coplanar spherical shells , of radii 'a' and 'b' (b>a), carry charges q and Q respectively. Find the magnitude of the electric at a point distant x from their common centre for
0<x<a,
(b) a≤x≤b,
(c) b≤x<∞View SolutionA coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) r>a, (b) a<r<b and (c) b>r>c
 View Solution
View SolutionA current I flows radius along a lengthy thin-walled tube of radisu R with longiitual slit of width h. Find the induction of the magnietic field inside the tube under the condition h<<R
View SolutionThere are two co-axial non conducting cylinders of radii a and b(>a). Length of each cylinder is L(>>b) and their curved surfaces have uniform surface charge densities of–σ (on cylinder of radius a) and +σ (on cylinder of radius b). The two cylinders are made to rotate with same angular velocity ω as shown in the figure. The charge distribution does not change due to rotation. Find the electric field (E) and magnetic field (B) at a point (P) which is at a distance r from the axis such that (a) 0<r<a (b) a<r<b (c) r>b. Assume that point P is close to perpendicular bisector of the length of the cylinders
 View Solution
View Solution

