Four point charges $+ 8 m C$ , $- m C$ , and $+ 8 m C$ are fixed at the points $- \sqrt{\frac{27}{2}} m$ , $- \sqrt{\frac{3}{2}} m$ , +sqrt(3/2)m $and$ +sqrt(27/2)m $r e s p e c t i v e l y o n t h e y - a ξ s . A p a r t i c \leq o f m a s s$ 6xx10^-4kg $and c h a r \geq$ +0.1muC $m o v e s a l o n g t h e - x d i r e c t i o n . I t s s p e e d a t$ x=+oo $i s$ V_0 $. F \in d t h e \leq * v a l u e o f$ V_0 $f or w h i c h t h e p a r t i c \leq w i l l c r o s s t h e or i g \in . F \in d a l s o t h e k \in e t i c e \neq r g y o f t h e p a r t i c \leq a t t h e or i g \in . A s \sum e t ˆ s p a c e i s g r a v i t y e e . < b r > G i v e n$ (1)/(4piepsilon_0)=9xx10^9Nm^2//C^2.

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Let the particle at some instant be at a point P distant x from the origin. As shown in the figure, there are two forces of repulsion acting due to two charges of +8 mC. The net force is $2 F cos α$ towards light.
Similarly there are two forces of attraction due to two charges of $- 1 m C$ . The net force due to these force is $2 F cos β$ towards left.

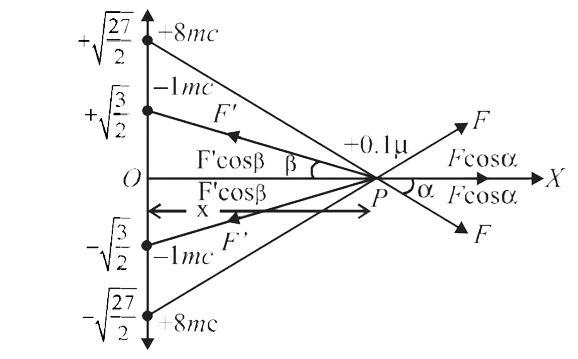
The net force on charge $0.1 μ C$ is zero when
$2 F cos α = 2 F^{'} cos β$
$\frac{K \times 8 \times 10^{- 6} \times 0.1 \times 10^{- 6}}{{(\sqrt{x^{2} + \frac{27}{2}})}^{2}} \times \frac{x}{\sqrt{x^{2} + \frac{27}{2}}}$
$= \frac{K \times 1 \times 10^{- 6} \times 0.1 \times 10^{- 6}}{{(\sqrt{x^{2} + \frac{3}{2}})}^{2}} \times \frac{x}{\sqrt{x^{2} + \frac{3}{2}}}$
$\Rightarrow x = \pm \sqrt{\frac{5}{2}}$
This means that we need to move the charge from $- \infty$ to $\sqrt{\frac{5}{2}}$ . Thereafter the attractive forces will make the charge move to origin.
The electric potential of the four charges at $x = \sqrt{\frac{5}{2}}$ is
$V = \frac{2 \times 9 \times 10^{9} \times 8 \times 10^{- 6}}{\sqrt{\frac{5}{2}} + \frac{27}{2}}$ -(2xx9xx10^9xx10^-6)/(sqrt(5/2)+3/2) $< b r >$ =2xx9xx10^9xx10^-6[8/4-1/2]=2.7xx10^4V $< b r > K \in e t i c e \neq r g y i s r e q u i r e d \to o v e r c o m e t h e f or c e o f r e p s - i o n o m$ prop $\to$ x=sqrt(5/2) $. < b r > T h e w or k d o \neq \in t h i s p r o c e s s i s$ W=q(V) $< b r > w h e r e V = p . d b e t w e e n$ oo $and$ x=sqrt(5/2) $. < b r >$ :.W=0.1xx10^-6xx2.7xx10^4=2.7xx10^-3J $< b r > B y e \neq r g y c o n s e r v a t i o n$ 1/2mV_0^2=2.7xx10^-3 $< b r >$ implies 1/2xx6xx10^-4V_0^2=2.7xx10^-3 $< b r >$ implies V_0=3m//s $< b r > K . E . a t t h e or i g \in < b r > P o t e n t i a l a t or i g \in$ V_(x=0)=(2xx9xx10^9xx8xx10^-6)/(sqrt(27/2))-(2xx9xx10^9xx10^-6)/(sqrt(3/2)) $< b r >$ =2.4xx10^4 $< b r > A g a \in b y e \neq r g y c o n s e r v a t i o n < b r >$ K.E. =q[V_(x=(sqrt5)/(2))-V_(x=0)] $< b r >$ :. $K . E . = 0.1 \times 10^{- 6} [2.7 \times 10^{4} - 2.4 \times 10^{4}]$
$= 0.1 \times 10^{- 6} \times 0.3 \times 10^{4}$
$= 3 \times 10^{- 4} J$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Four point charges q, -2q, -q and 2q are placed at points (0,0,0) m , $(\sqrt{2}, 0, 0) m, (\sqrt{2}, \sqrt{2}, 0) m and (0, \sqrt{2}, 0)$ m respectively . The electric field at point $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0) m is (q = 1 μ C)$
A $18 \times 10^{3} N / C$
B $36 \times 10^{3} N / C$
C $18 \sqrt{5} \times 10^{3} N / C$
D $18 \sqrt{3} \times 10^{3} N / C$
A particle of mass $m = 5 k g$ is moving with a uniform speed $v = 3 \sqrt{2}$ in the $X O Y$ plane along the line $Y = X + 4$ . The magnitude of the angular momentum of the particle about the origin is
A $60$ unit
B $40 \sqrt{2}$ unit
Czero
D $7.5$ unit
A particle of mass 2 g and charge $1 μ C$ is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
A100 m/s
B90 m/s
C60 m/s
D45 m/s

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-ELECTROSTATICS-Subjective Problems

Home
Ask Doubt
Profile