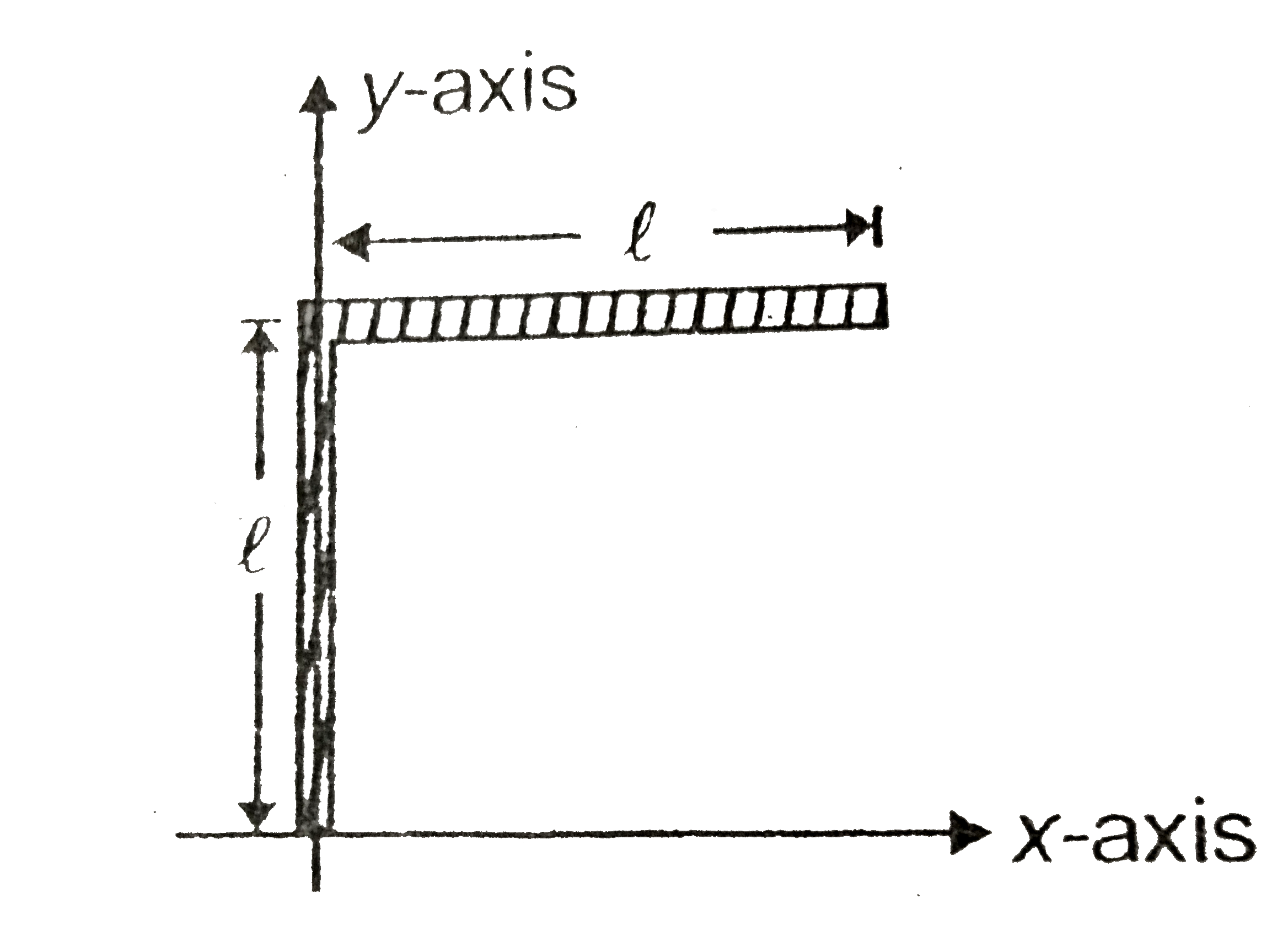Consider the object shown in the figure. It consist of a solid hemisphere of mass M and radius R. There is a solid rod welded at its centre. The object is placed on a flat surface so that the rod is vertical. Mass of the rod per unit length is $\frac{M}{2 R}$ . What is the maximum length of the rod that can be welded so that the object can perform oscillations about the position shown in diagram?
Note : Centre of mass of a solid hemisphere is at a distance of $\frac{3 R}{8}$ from its base.

Text Solution

Verified by Experts

The correct Answer is:Less than $\sqrt{\frac{3}{2}} R$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cylinder is of the height 8 m and has base radius 8 m. The maximum length of the rod that can be placed in it is
A $8 \sqrt{5} m$
B $9 \sqrt{5} m$
C $8 \sqrt{3}$ m
D $8 (2 π + 1) m$
Question 2 - Select One
A cylinder is of the height 8 m and has base radius 8 m. The maximum length of the rod that can be placed in it is
A $8 \sqrt{5} m$
B $9 \sqrt{5} m$
C $8 \sqrt{3} c m$
D $8 (2 π + 1) m$
Question 3 - Select One
A thin rod of length $L$ is bent to form a semi circle. The mass of the rod is $M$ . What will be the gravitational potential at the centre of the circle?
A $\frac{- G M}{L}$
B $\frac{- G M}{2 π L}$
C $\frac{- π G M}{2 L}$
D $\frac{- π G M}{L}$

ARIHANT-ROTATIONAL MOTION-PHYSICS

Home
Ask Doubt
Profile