A uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is μ=0.3.
Find the angle ϕ that the circular base of the hemisphere makes with the horizontal.
Given sin(tan−10.3)≅0.29 and sin−1(0.77)≅50∘
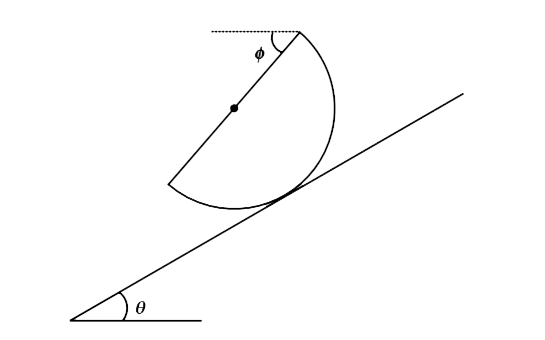
The correct Answer is:50∘
Step by step video, text & image solution for A uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is mu = 0.3. Find the angle phi that the circular base of the hemisphere makes with the horizontal. Given sin (tan^(-1) 0.3) cong 0.29 " and "sin^(-1) (0.77) cong 50^(@) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View Solution
Knowledge Check
A plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2A plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of does not slide is:
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
AR2B(1−√32)RC√32RD3R8
A solid homigeneous hemisphere rests on a rough horizontal plane and against a smooth vertical wall. If the coefficient of friction is greater than 38, the hemisphere can rest in any position and if it is less, the least angle that the base of the hemisphere can make with the vertical is cos−1(8μ3). If the wall be rough, the coefficient of friction μ, this angle is cos−1(8μ3.1+μ'1+μμ') .
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution