A uniform meter stick AB of mass M is lying in state of rest on a rough horizontal plane. A small block of mass m is placed on it at its centre C. A variable force F is applied at the end B of the stick so as to rotate the stick slowly about A in vertical plane. The force F always remains perpendicular to the length of the stick. The stick is raised to θ=60∘ and it was observed that neither the end A slipped on the ground nor the block of mass m slipped on the stick.
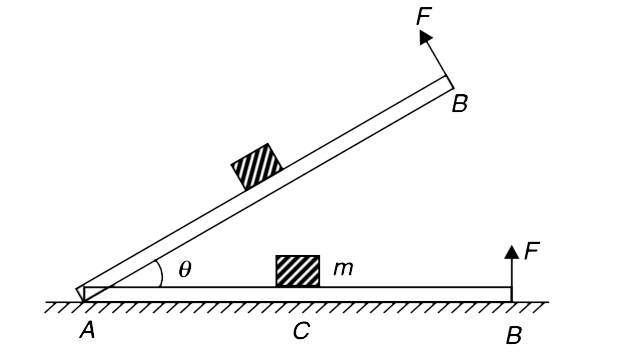
(a) F1 is force applied by the stick on the block. Plot the variation of F1 with θ(0≤θ≤60∘).
(b) What must be the minimum coefficient of friction between the block and the stick.
(c) f is the friction force acting at end A of the stick. Plot variation of fvsθ(0∘≤θ≤60∘).
The correct Answer is:(a) (##IJAPHYV01C06E01082_A01##)
(b) μmin=√3
(c) (##IJAPHYV01C06E01082_A02##)
Topper's Solved these Questions
Similar Questions
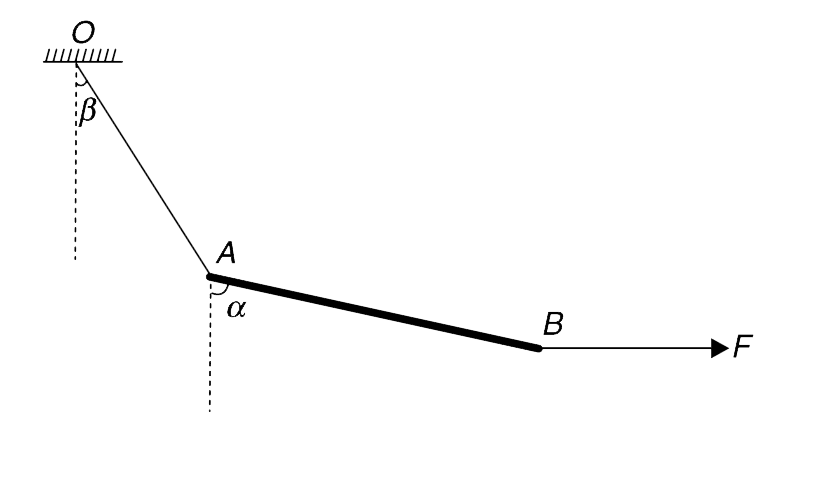
A stick AB of mass M is tied at one end to a light string OA. A horizontal force F=Mg is applied at end B of the stick and its remains in equilibrium in position shown. Calculate angles α and β.
View SolutionA uniform stick of mass M and length L is kept vertical on a frictionless horizontal floor. If the stick is allowed to fall, then mark the correct alternatives
View Solution
Knowledge Check
The M.I. of a thin uniform stick of mass 9 gm about an axis passing through one end perpendicular to the length of a meter stick is
A90gmcm2B9kgm2C3gmm2D9.8kgm2A uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
Aangular velocity of the system after collision is 25vlBangular velocity of the system after collision is v2lCThe loss in kinetic energy of the system as a whole as a result of the collision 310mv2DThe loss in kinetic energy of the system as a whole as a result of the collision 7mv224
A uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm fomd the left end. Find the tensions in the two strings.
View SolutionA uniform metre stick of mass 200 g is suspended from the ceiling through two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
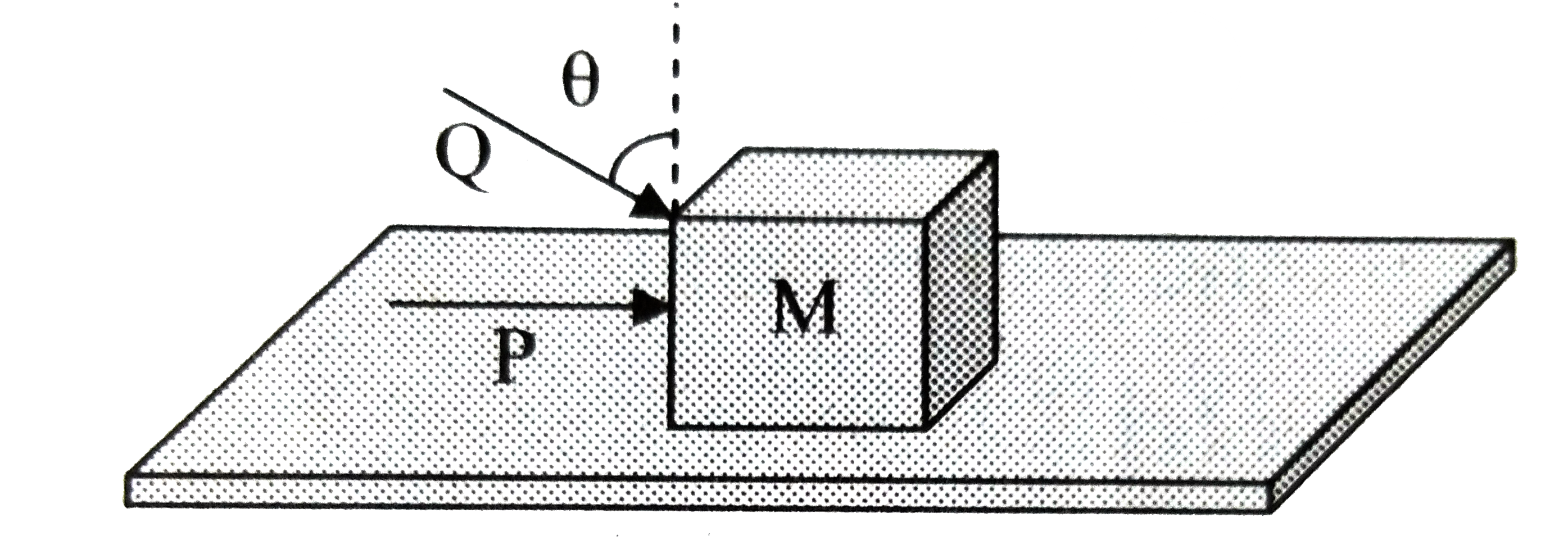
View Solution
