Two identical positive charges Q each are placed on the x axis at point (-a,0) and (a,0) A point charge of magnitude q is placed at the origin. For small displacement along x axis, the charge q executes simple harmonic motion if it is poitive and its time period is T1. if the charge q is negative, it perform oscillations when displaced along y axis. in this case the time period of small oscillations is T2. find T1T2
The correct Answer is:1√2
To solve the problem, we need to analyze the forces acting on the charge q when it is displaced along the x-axis and y-axis. We will derive the time periods T1 and T2 for the respective cases and then find the ratio T1T2.
1. Understanding the Setup:
- We have two identical positive charges Q located at points (−a,0) and (a,0).
- A point charge q is placed at the origin (0,0).
- We will analyze the forces acting on q when it is displaced along the x-axis and y-axis.
2. Case 1: Positive Charge q Displaced Along the x-axis:
- When the charge q is displaced by a small distance x along the x-axis, the distances from the charges become A+x and A−x.
- The forces due to the two charges can be expressed as:
F1=kQq(a+x)2,F2=kQq(a−x)2
- The net force F acting on q can be calculated as:
F=F1−F2=kQq(a+x)2−kQq(a−x)2
- Using the binomial approximation for small x (i.e., (a+x)−2≈1a2−2xa3), we can simplify the expression for F:
F≈−4kQqa3x
- This indicates that the motion is simple harmonic with:
F=−keffxwhere keff=4kQqa3
- The angular frequency ω is given by:
ω2=keffm=4kQqma3
- Therefore, the time period T1 is:
T1=2π√mkeff=2π√ma34kQq=2π√4kQq√ma3
3. Case 2: Negative Charge q Displaced Along the y-axis:
- When the charge q is displaced by a small distance y along the y-axis, the distance from the charges becomes √a2+y2.
- The forces acting on q due to the two charges can be expressed as:
F=2⋅kQ(−q)(a2+y2)⋅y√a2+y2(only vertical components add)
- For small y, we can approximate √a2+y2≈a:
F≈−2kQqa3y
- This also indicates simple harmonic motion with:
keff=2kQqa3
- The angular frequency ω is given by:
ω2=2kQqma3
- Therefore, the time period T2 is:
T2=2π√mkeff=2π√ma32kQq=2π√2kQq√ma3
4. Finding the Ratio T1T2:
- Now we can find the ratio:
T1T2=2π√4kQq√ma32π√2kQq√ma3=√2√4=1√2
Final Answer:
T1T2=1√2
- We have two identical positive charges Q located at points (−a,0) and (a,0).
- A point charge q is placed at the origin (0,0).
- We will analyze the forces acting on q when it is displaced along the x-axis and y-axis.
- When the charge q is displaced by a small distance x along the x-axis, the distances from the charges become A+x and A−x.
- The forces due to the two charges can be expressed as:
F1=kQq(a+x)2,F2=kQq(a−x)2
- The net force F acting on q can be calculated as:
F=F1−F2=kQq(a+x)2−kQq(a−x)2
- Using the binomial approximation for small x (i.e., (a+x)−2≈1a2−2xa3), we can simplify the expression for F:
F≈−4kQqa3x
- This indicates that the motion is simple harmonic with:
F=−keffxwhere keff=4kQqa3
- The angular frequency ω is given by:
ω2=keffm=4kQqma3
- Therefore, the time period T1 is:
T1=2π√mkeff=2π√ma34kQq=2π√4kQq√ma3
- When the charge q is displaced by a small distance y along the y-axis, the distance from the charges becomes √a2+y2.
- The forces acting on q due to the two charges can be expressed as:
F=2⋅kQ(−q)(a2+y2)⋅y√a2+y2(only vertical components add)
- For small y, we can approximate √a2+y2≈a:
F≈−2kQqa3y
- This also indicates simple harmonic motion with:
keff=2kQqa3
- The angular frequency ω is given by:
ω2=2kQqma3
- Therefore, the time period T2 is:
T2=2π√mkeff=2π√ma32kQq=2π√2kQq√ma3
- Now we can find the ratio:
T1T2=2π√4kQq√ma32π√2kQq√ma3=√2√4=1√2
T1T2=1√2
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 359videos
ELECTROSTATICS
- BOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 359videos
ELECTROSTATICS
- BOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 312videos
ELECTROMAGNETIC INDUCTION
- BOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 39videos
GEOMETRICAL OPTICS
Similar Questions
Three small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
03:45View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
04:53View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
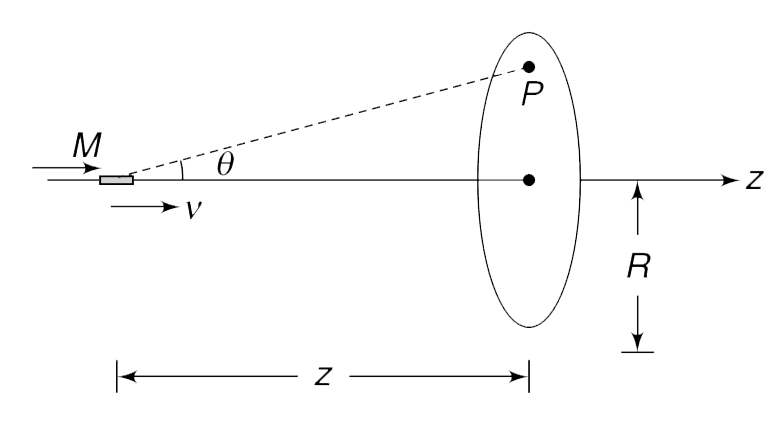
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
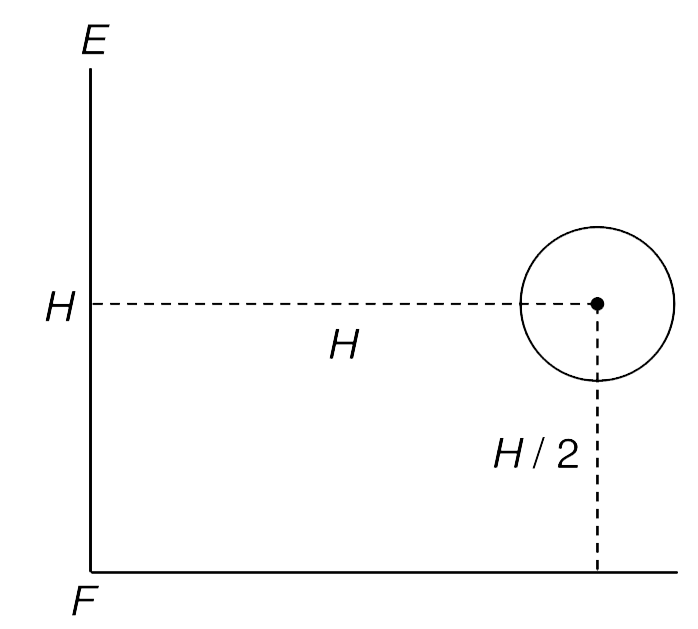
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.04:32View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
 05:55View Solution
05:55View SolutionTwo point charges +q and fixed at (a,0,0) and (-a,0,0) . A third point charge -q is at origin. State whether ite equlilbrium is stable, unstable or neutral if it is slightly displaced: (a) along x-axis. , (b) along y-axis.
View SolutionTwo indentical point charges having magnitude q each are placed as shown if fig. If we place a negative cahrge (of magnitude -q and mass m)at the midpoint of charges and displaced along the x-axis, examine whether it will perform simpe harmonic motion. If yes then find the time period of oscillation of the particle.
 06:51View Solution
06:51View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the sme polarity can move along the x-axis. Then
09:17View Solutiontwo similar point charge + q are kept on x- axis at (-a,0)& (a,0) and another charge -Q of mass m Is kept at origin .If -Q si slightly displaced along y- axis & released them its time period of oscillation is -
06:51View SolutionTwo point charge (Q each) are placed at (0,y) and (0,-y). A point charge q of the same polarity can move along X-axis. Then :
05:37View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis. At the origin, charge q' will be in
View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis. Speed of charge q' at infinity is
03:55View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be in13:21View SolutionTwo equal negative charges -q are fixed at the points (0,alpha) and (0, -alpha) on the y-axis. A positive charge Q is released from rest at the point (2alpha, 0) on the x-axis. The charge Q will
06:36View SolutionTwo equal negative charges -q are fixed at point (0, a) and (0, -a). A positive charge Q is released from rest at the point (2a, 0) on the x-axis. What type of oscillations does the charge Q execute?
08:58View Solutionदो समान ऋण आवेश q, q, Y-अक्ष पर बिंदुओं (0, a) तथा (0,−a) पर स्थित है। एक धन आवेश Q, X-अक्ष पर बिंदु (2a,0) पर विरामावस्था से मुक्त किया जाता है। आवेश Q
05:54View Solution

