The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
The correct Answer is:(a). V=σ8∈0[√R2+Z2−Z]
(b). EZ=σ8∈0[1−Z√R2+Z2]
Step by step video, text & image solution for The quarter disc of radius R (see figure) has a uniform surface charge density sigma. (a) Find electric potential at a point (O,O,Z) (b). Find the Z component of electrif field at (O,O,Z) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
Knowledge Check
The electric field inside a spherical shell of uniform surface charge density is
AZeroBConstantCProportional to the distance from the centreDIrregularA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
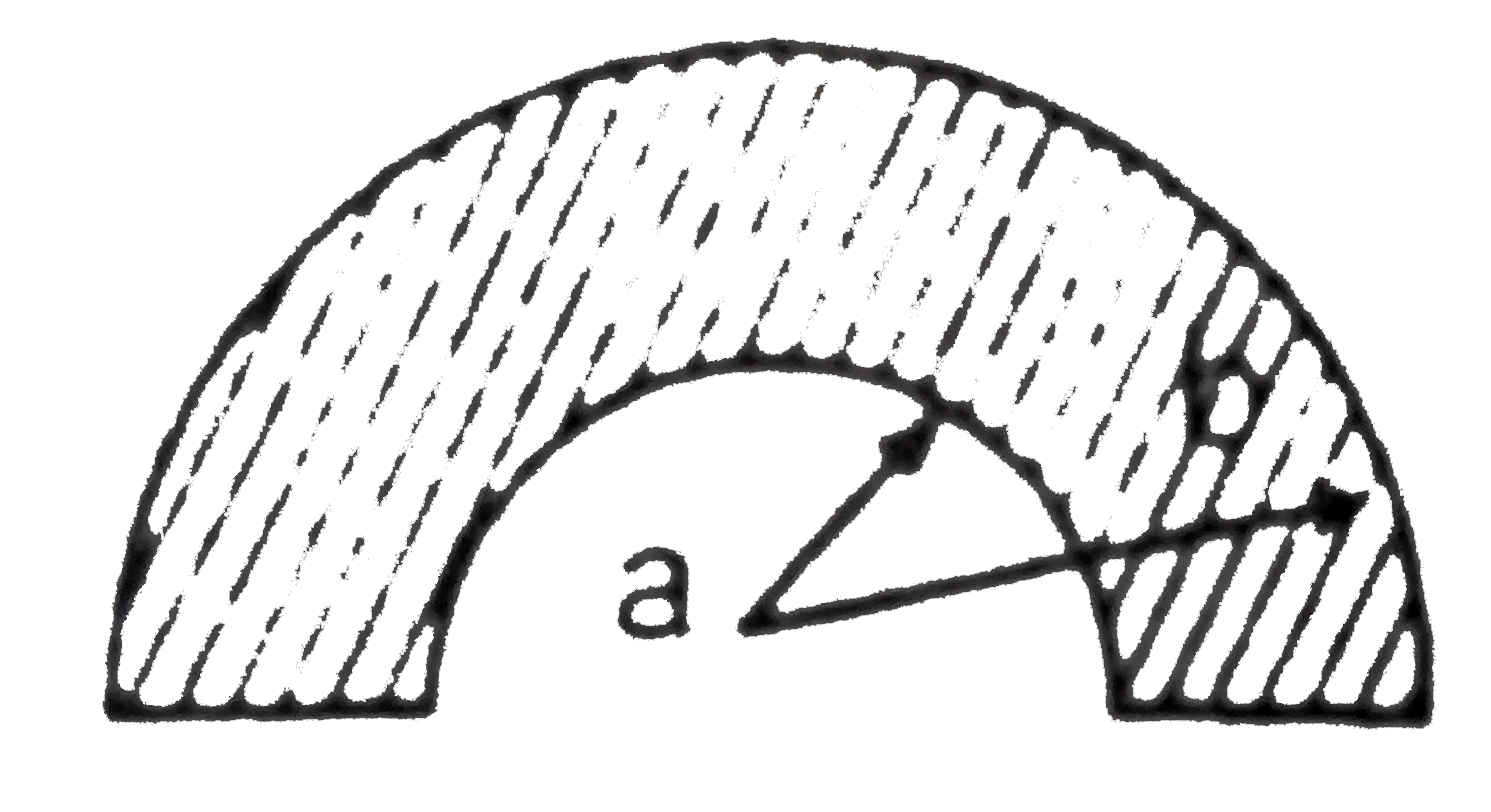 A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
A1πlnb/a(b−a)B2πC1πln(b/a)2(b−a)Dπ(b−a)2ln(b/a)
There is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionA uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
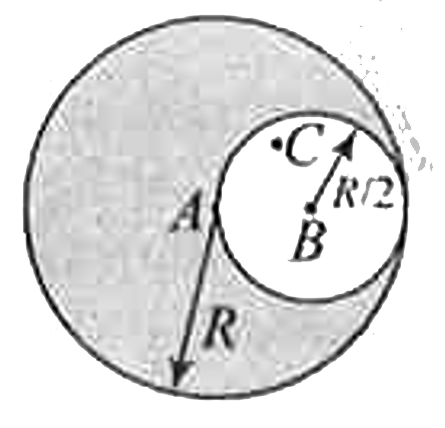
View SolutionThe diagram shows a part of disc of radius R carrying uniformly distributed charge of density σ. Electric potential at the centre O of parent disc is
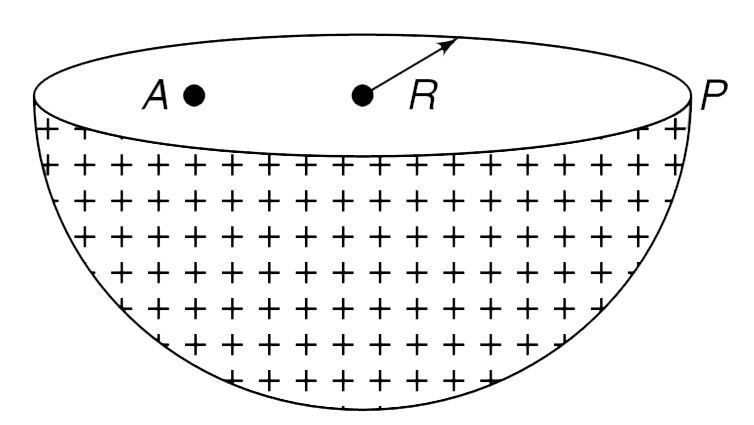
View SolutionA hemispherical bowl of radius R carries a uniform surface charge density of σ. Find potential at a point P located just outside the rim of the bowl (see figure). Also calculate the potential at a point A located at a distance R/2 from the centre on the equatorial plane.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution