A hemispherical bowl of radius R carries a uniform surface charge density of σ. Find potential at a point P located just outside the rim of the bowl (see figure). Also calculate the potential at a point A located at a distance R/2 from the centre on the equatorial plane.
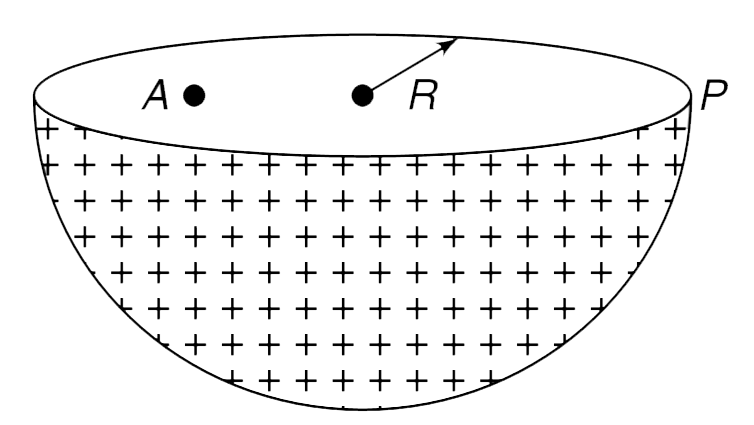
The correct Answer is:At both P and A the potential is σR2ε0
Topper's Solved these Questions
Similar Questions
A hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
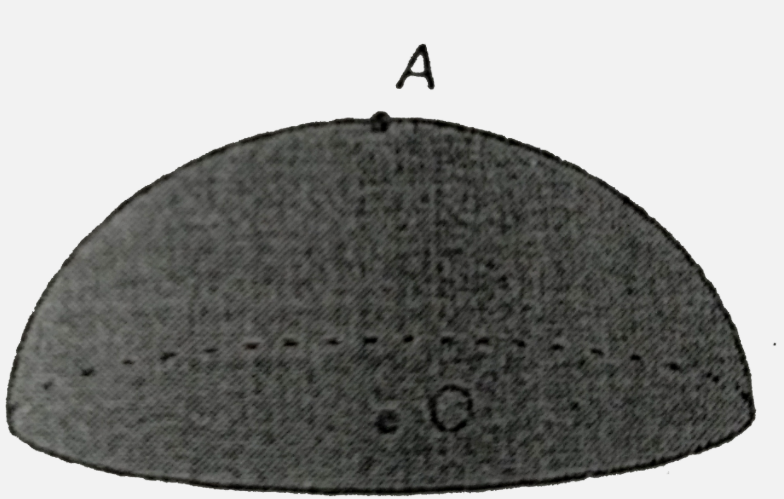
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2
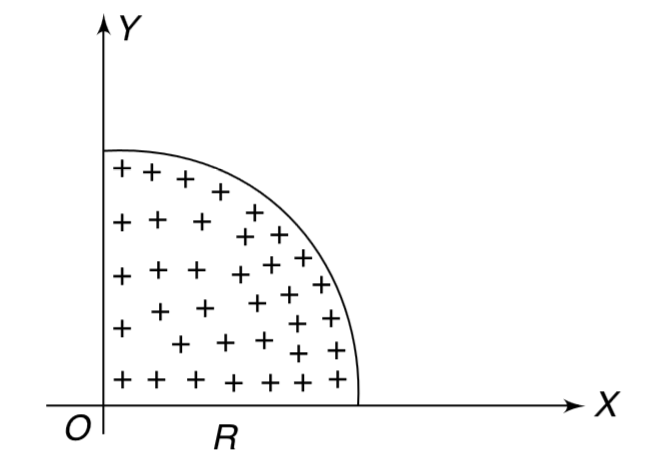
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
View Solution
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
View SolutionA sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionA uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View Solution
