The fig shows a network consisting of an infinite number of pairs of resistors $R_{1} = 2 Ω and R_{2} = 1 Ω$ . Since the network is infinite, removing a pair of $R_{1} and R_{2}$ from either end of the network will not make any difference. Using this calculate the equivalent $(R)$ across points A and B.

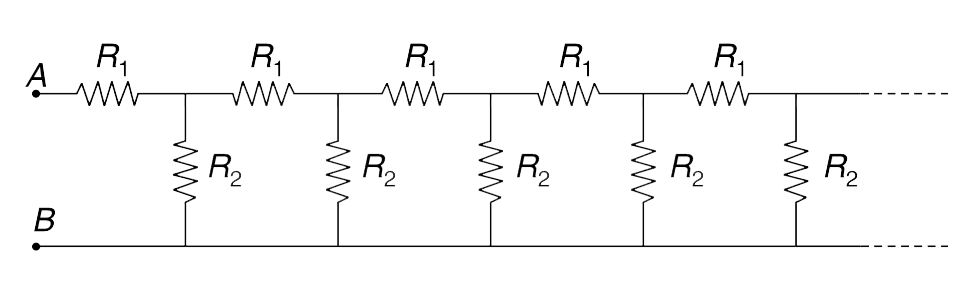
(b) Prove that $I_{n} = \frac{I_{n - 1} R_{2}}{R_{2} + R} = \frac{I_{n - 1}}{\sqrt{3} + 2}$ ltbr Where $I_{n}$ and $I_{n - 1}$ represent the current through $R_{1}$ in $n^{t h}$ and ${(n - 1)}^{t h}$ segment respectively (see Fig)

(c) If a 20 V battery is connected across A and B find $I_{10}$

Text Solution

Verified by Experts

The correct Answer is:(a) $R = (1 + \sqrt{3}) Ω$
(c) $\frac{20}{(\sqrt{3} - 1) {(\sqrt{3} + 2)}^{9}}$

Updated on:21/07/2023

In the given network, the powers generated in the resistor $R_{1}$ and $R_{2}$ are $P_{1}$ and $P_{2}$ and the power generated in $R$ is P. For this network.
Aif $P_{1} = P_{2}$ it necessarily follows that $R_{1} = R_{2}$
Bif $R = R_{1} + R_{2}$ , then $P > P_{1} + P_{2}$
Cif $P = P_{1} + P_{2}$ then $R \leq \frac{R_{1} + R_{2}}{4}$
Dif $R_{1} = R_{2}$ then it necessarily follows that $P = P_{1} + P_{2}$
In the circuit shown in adjoining fig E =10V, $R_{1} = 1 Ω R_{2} = 2 Ω, R_{3} = 3 Ω and L = 2 H$ . Calculate the value of current $i_{1}, i_{2} and i_{3}$ immidiately after key S is closed :-

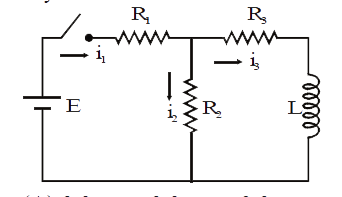A3.3 amp, 3.3 amp, 3.3 amp
B3.3 amp, 3.3 amp, 0 amp
C3.3 amp, 0 amp, 0 amp
D3.3 amp , 3.3 amp 1.1 amp