In the last problem calculate the amount of heat dissipated in the resistance assuming that the time constant of the circuit is very small and the discharge process is almost instantaneous.
The correct Answer is:
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor has its two plates connected to an ideal spring of force constant K. Relaxed length of spring is L and it is made of non conducting material. The area of each plate is A. The capacitor has a charge q0 on it. To discharge the capacitor through the resistance R, switch S is closed.
If the time constant of the circuit is very large and discharge process is very slow, how much heat will be dissipated in the resistance? Assume that there is no friction and the plates always remains parallel to each other.
View SolutionA charged capacitor of capacitance 40μF is discharged through a 50Ω resistance. Determine the time constant of the circuit.
View Solution
Knowledge Check
A capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
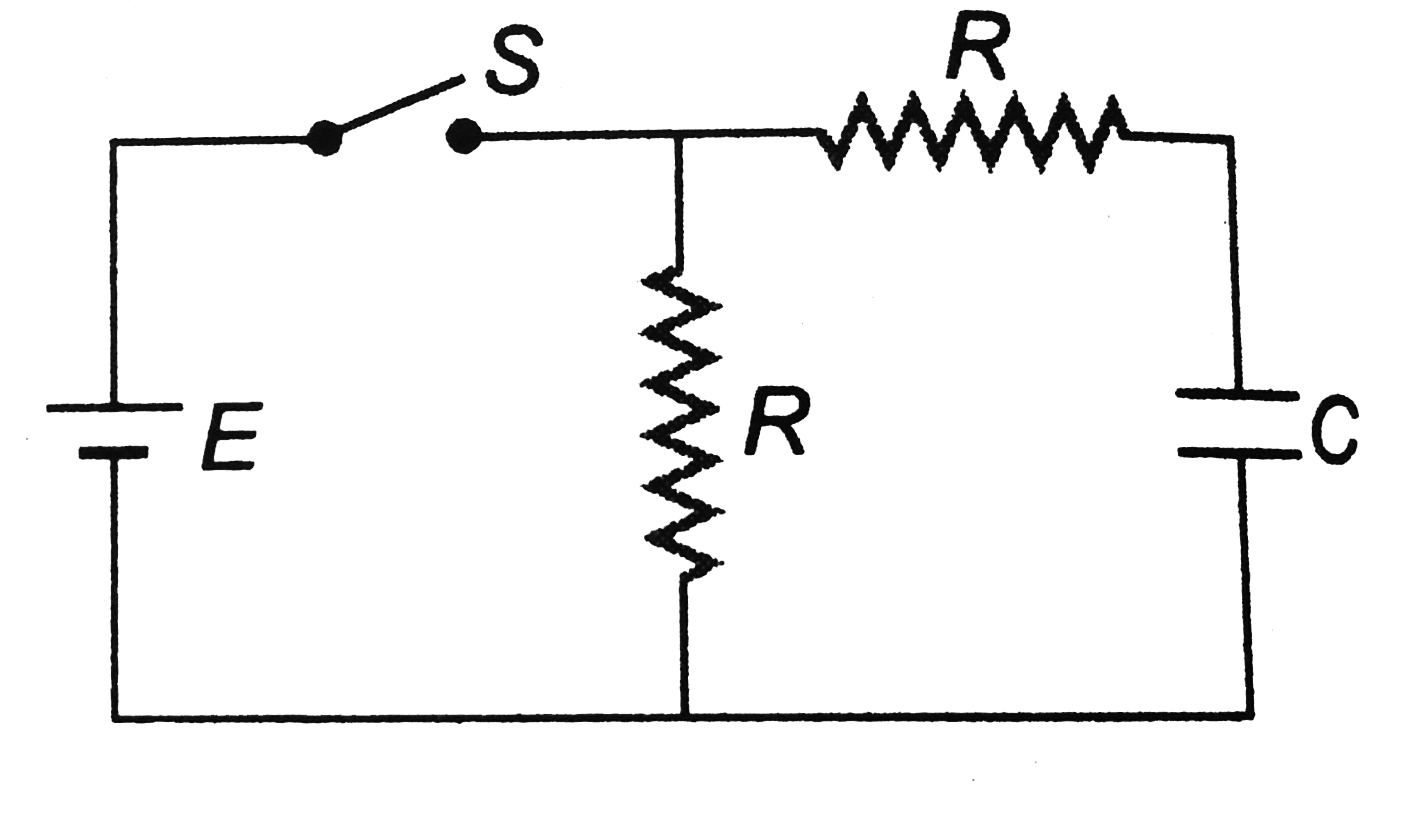
i. At the time of charging of capacitor time constant of the circuit is 2CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CRAstatements i and ii only are correctBstatements ii and iii only are correctCstatements iii and iv only are correctDstatements i and iii only are correctA charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
AηB2ηCη2DzeroWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0
AThe initial charge on the capacitor was i0τBThe initial charge on the capacitor was 12i0τCThe initial energy stored in the capacitor was i20τDThe initial energy stored in the capacitor was 12i20Rτ
A capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets

i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View SolutionA charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
View SolutionA charged capacitor C1 is discharged through a resistance R by putting switch S in position 1 of the circuit as shown in fig.5.201. When the discharge current reduces to i0, the switch is suddenly shifted to position 2. Calculate the amount of heat liberated in resistor R starting form this instant. Also calculate current I through the circuit as a function of time.

View SolutionAn inductor coil stores U energy when i current is passed through it and dissipates energy at the rate of P. The time constant of the circuit, when this coil is connected across a battery of zero internal resistance is
View SolutionAn inductor coil stores U energy when i current is passed through it and dissipates energy at the rate of P. The time constant of the circuit, when this coil is connected across a battery of zero internal resistance is
View Solution
