An inertial frame of reference is, by definition,
a frame moving with uniform velocity w.r.t. earth
a frame moving with velocity w.r.t our Sun
a frame which is not rotating
a frame in which Newton's first law of motion is valid.
The correct Answer is:D
Step by step video, text & image solution for An inertial frame of reference is, by definition, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
Non-inertial frame of reference have
Azero acceleration.Bsome acceleration with respect to inertial frame of reference.Czero velocity.Dconstant velocity with respect to inertial frame of reference. - Question 2 - Select One
In an inertial frame of reference, a body performing uniform circular motion in clockwise direction has
Aconstant velocityBzero angular accelerationCcentripetal accelerationDtangential acceleration - Question 3 - Select One
Assertion :− Newton's first law defines inertial frame of reference.
Reason :− Newton's laws can be applied only in inertial frames of reference.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False
It is sometimes heard that inertial frame of reference is only an ideal concept and no such inertial frame actually exists. Comment.
View SolutionA particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
View SolutionFrame OF References
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
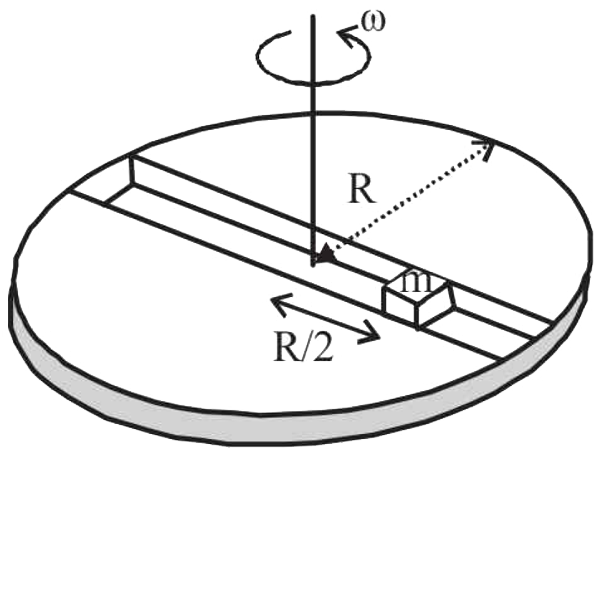
The distance r of the block at time isView SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
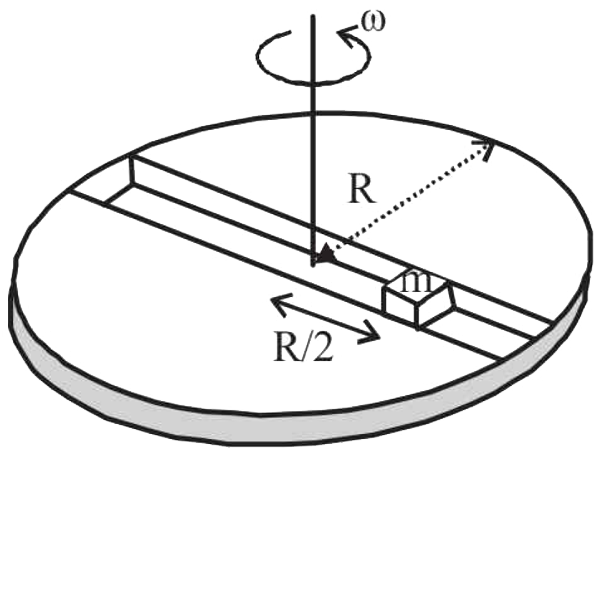
The net reaction of the disc on the block isView Solution

