Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.
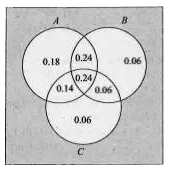
Which of the following is not true ?
A and B are independent
B and C are independent
A and C are independent
A and B∩C are independent
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
The following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.

View SolutionProve the following A∩(B−C)=(A∩B)−(A∩C)
View Solution
Knowledge Check
Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
P(A∩B'∩C')=0.18 , P(A'∩B∩C')= 0.06 etc.

Which of the following is not true ?AA and B are independentBB and C are independentCA and C are independentDA and B∩C are independentLet A,B and C be sets such that A∩B⊆C and A∩B≠ϕ. Then which of the following statements is not true?
AB∩C≠ϕBIf (A−B)⊆C, then A⊆CCC(∪A)∩(C∪B)=CDIf (A−C)⊆B, then A⊆BFor two given events A and B P(A∩B)=
ANot less than P(A) + P(B) -1BNot greater than P(A) + P(B)CEqual to P(A)+P(B)−P(A∪B)DAll of the above
Event A and B are such that P(A)=0.5,P(B)=0.25 and P(A∩B)=0.125. Find P(A'∩B').
View SolutionIf A, B and C be sets. Then, show that A∩(B∪C)=(A∩B)∪(A∩C).
View SolutionIf P(A) = 0.7, P(B) = 0.4, P(A∩B) = 0.3, then P(A∩B')=
View SolutionIf events are independents and P(A)=13,P(B)=13 and P(C)=14, then P(A'∩B'∩C') is equal to
View SolutionIf A and B are events sucn that P(A)=0.3P(B)=0.2 and P(A∩B)=0.1 then P(¯¯¯A∩B)=?
View Solution

