A block of mass m is pushed up against a spring, compressing it a distance x, and the block is then released. The spring projects the block along a frictionaless horizontal surface, grving the block a speed v. The same spring projects a second block of mass 4m, giving it a speed 3v. What distance was the spring compressed in the second case ?
6x
x6
36x
12x
The correct Answer is:A
To solve the problem, we will use the principle of conservation of energy and the relationship between the spring potential energy and the kinetic energy of the blocks.
Step 1: Calculate the potential energy stored in the spring for the first block
The potential energy (PE) stored in a compressed spring is given by the formula:
PE=12kx2
where k is the spring constant and x is the compression distance.
For the first block of mass m that is compressed by a distance x:
PE1=12kx2
Step 2: Relate the potential energy to the kinetic energy of the first block
When the block is released, all the potential energy is converted into kinetic energy (KE):
KE1=12mv2
Setting the potential energy equal to the kinetic energy:
12kx2=12mv2
Step 3: Simplify the equation for the first block
We can cancel out the 12 from both sides:
kx2=mv2
Step 4: Calculate the potential energy stored in the spring for the second block
For the second block of mass 4m that is projected with speed 3v, the potential energy stored in the spring when compressed by a distance x2 is:
PE2=12kx22
Step 5: Relate the potential energy to the kinetic energy of the second block
The kinetic energy of the second block is:
KE2=12(4m)(3v)2=12(4m)(9v2)=18mv2
Setting the potential energy equal to the kinetic energy:
12kx22=18mv2
Step 6: Simplify the equation for the second block
Again, we can cancel out the 12:
kx22=36mv2
Step 7: Relate the two equations
From the first block, we have:
kx2=mv2(1)
From the second block, we have:
kx22=36mv2(2)
Step 8: Divide equation (2) by equation (1)
kx22kx2=36mv2mv2
This simplifies to:
x22x2=36
Step 9: Solve for x2
Taking the square root of both sides:
x2x=6
Thus,
x2=6x
Final Result
The distance the spring was compressed in the second case is:
x2=6x
The potential energy (PE) stored in a compressed spring is given by the formula:
PE=12kx2
where k is the spring constant and x is the compression distance.
PE1=12kx2
When the block is released, all the potential energy is converted into kinetic energy (KE):
KE1=12mv2
12kx2=12mv2
We can cancel out the 12 from both sides:
kx2=mv2
For the second block of mass 4m that is projected with speed 3v, the potential energy stored in the spring when compressed by a distance x2 is:
PE2=12kx22
The kinetic energy of the second block is:
KE2=12(4m)(3v)2=12(4m)(9v2)=18mv2
12kx22=18mv2
Again, we can cancel out the 12:
kx22=36mv2
From the first block, we have:
kx2=mv2(1)
From the second block, we have:
kx22=36mv2(2)
kx22kx2=36mv2mv2
This simplifies to:
x22x2=36
Taking the square root of both sides:
x2x=6
Thus,
x2=6x
The distance the spring was compressed in the second case is:
x2=6x
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View Solution
Knowledge Check
A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of theseThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
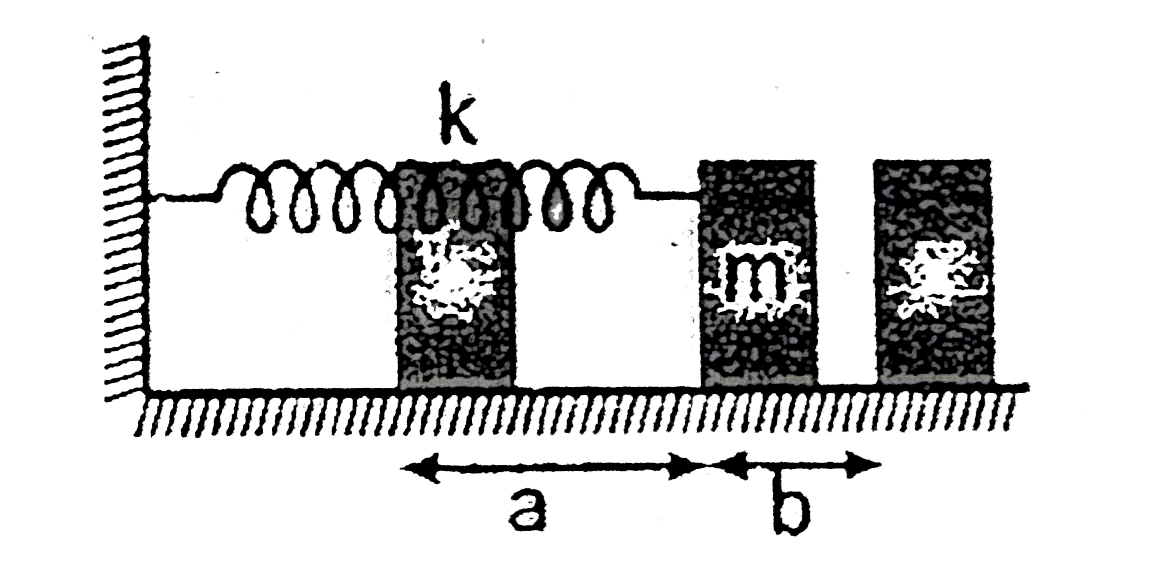 Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mg
Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mgA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. The spring constant of the spring is 6mv2nx2. Find value of n.
View SolutionA small block of mass 500 gm is pressed against a horizontal spring fixed at one end to a distance of 10 cm. when released, the block moves horizontally till it leaves the spring. Where it will hit the ground 5 m below the spring. (Take k = 100 N/m of spring)
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View Solution