A sector cut from a uniform disk of radius 12cm and a uniform rod of the same mass bent into shape of an arc are arranged facing each other as shown in the figure. If center of mass of the combination is at the origin, what is the raius of the arc?
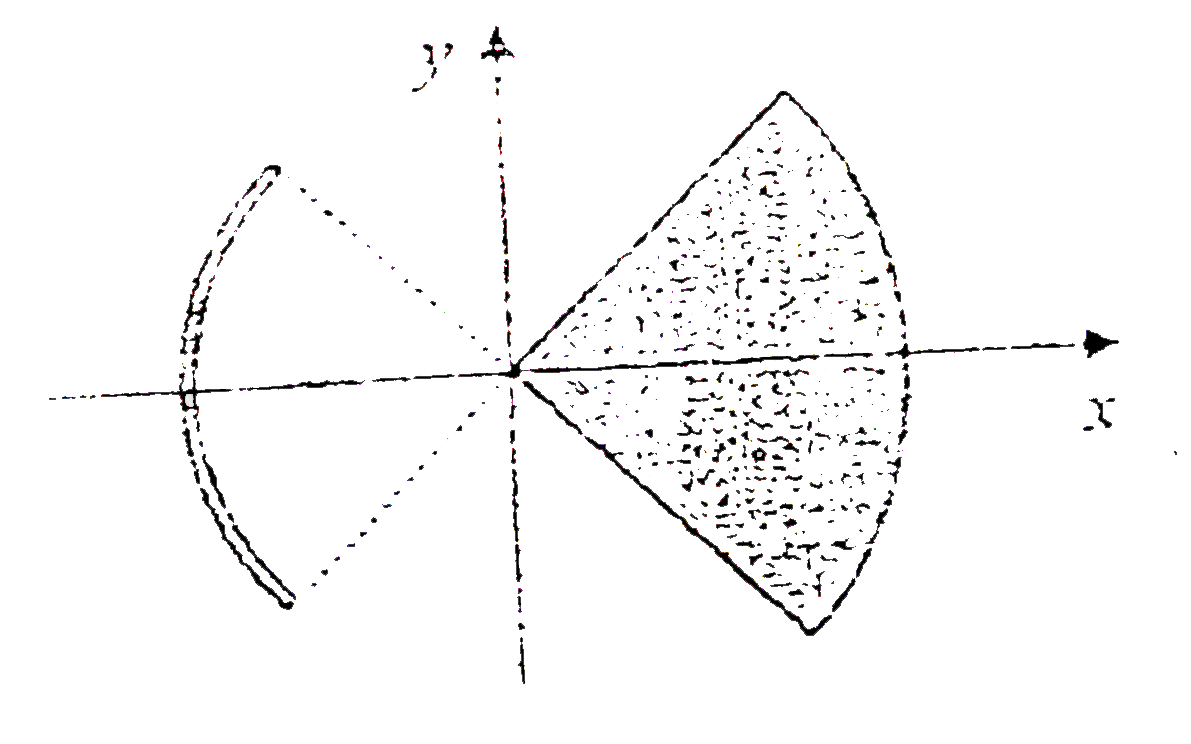
8cm
9cm
12cm
18cm
The correct Answer is:A
Ans.(1)
−MRsinθθ+M2×123sinθθ=0,
where θ is half angle R=8cm.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A uniform wire of length l and mass M is bent in the shape of a semicircle of radius r as shown in figure. Calculate moment of intertia about the axis XX'
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
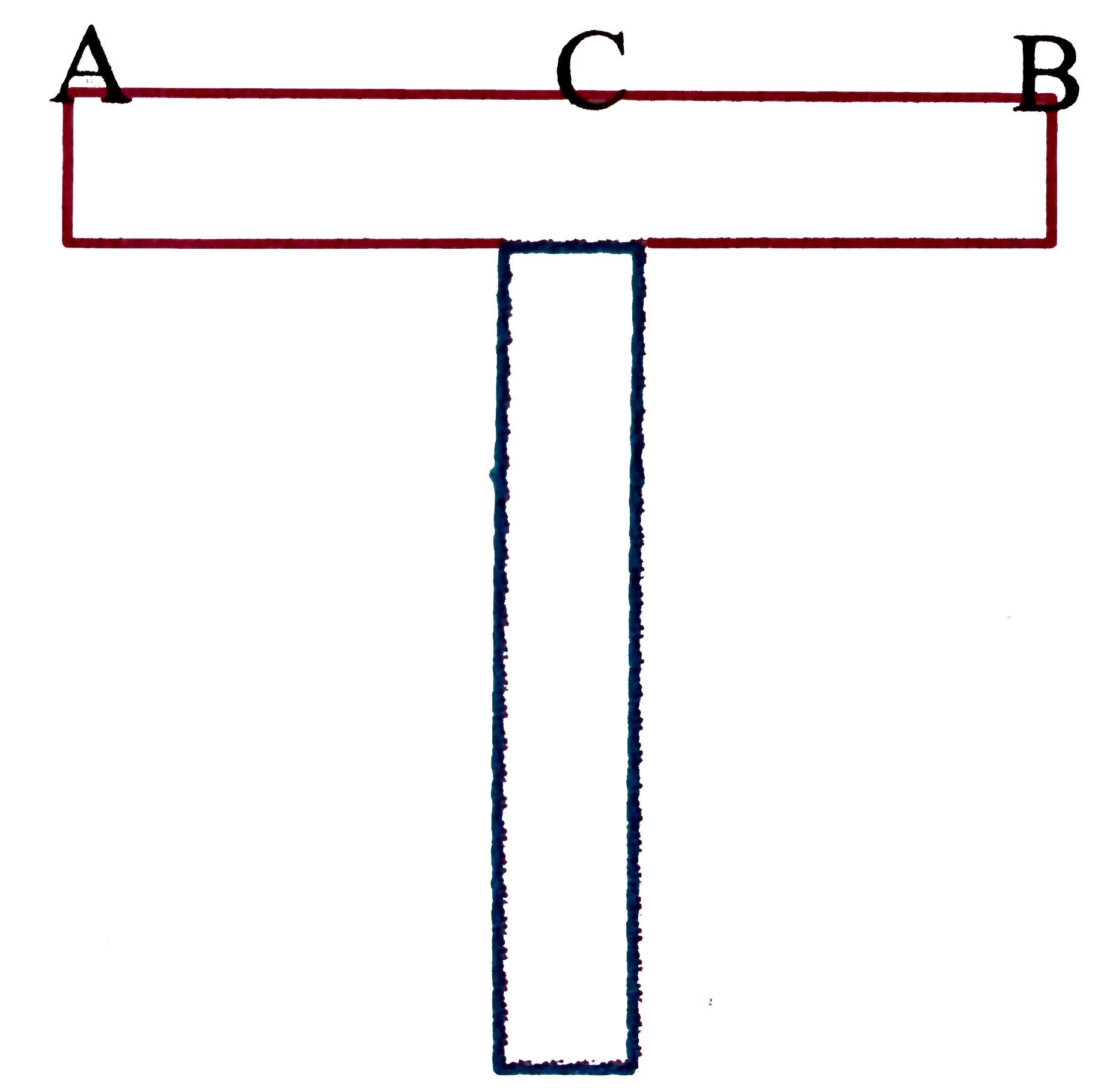 A0BL/4C3L/4DL
A0BL/4C3L/4DLA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)A uniform metre rod is bent into L shape with the bent arms at 90∘ to each other. The distance of the centre of mass from the bent point is
AL4√2mBL2√2mCL√2mDL8√2m
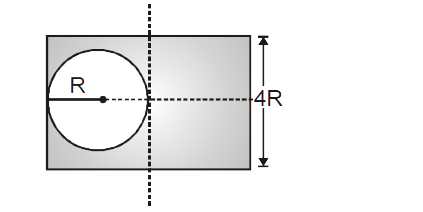
A circular hole with radius R/2 is carved from a uniform circular disk of radius R. A smaller disk with radius R/4 with the same uniform density is then put inside the hole as shown in the figure below. The center of mass of the whole system is located at a distance d from the origin. Find d. CM
View SolutionA uniform thin rod of length 3L is bent at right angles at a distance L from one end as shown in Fig. If length of rod is 1.8m, find the co-ordinates and position vector of the mass of the system.

View SolutionFind out the position of centre of mass of the uniform lamina as shown in figure.from center of cavity
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
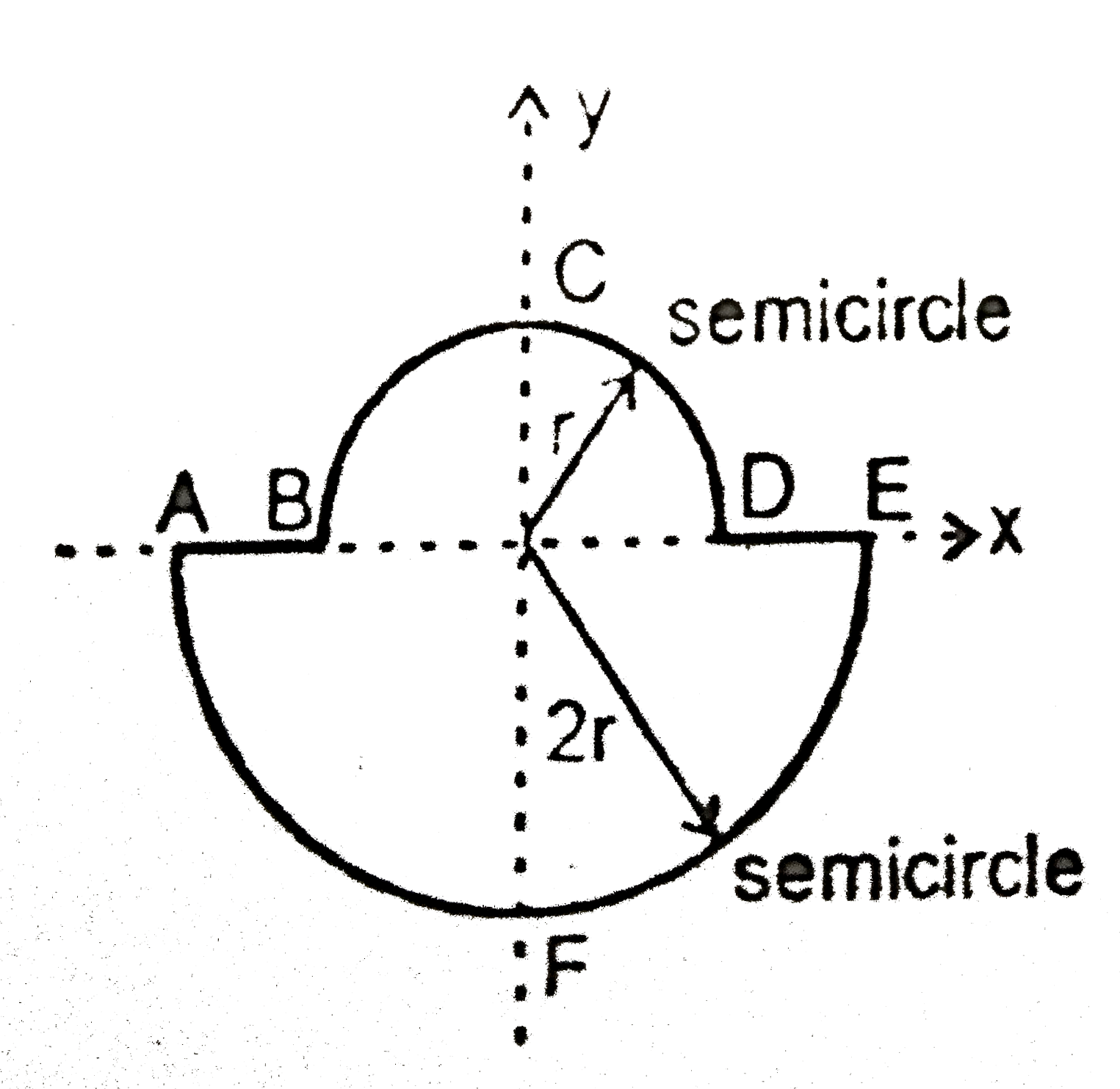
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View Solution
