Let A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
A
1:√2:√3
B
√2:√3:1
C
√3:1:√2
D
1:(√2−1):(√3−√2)
Video Solution
Text Solution
The correct Answer is:D
t1=√2hg
t2=√2×2hg
t3=√2×3hg
Required ratio t1:(t2−t1):(t3−t2)
=1:(√2−1):(√3−√2)
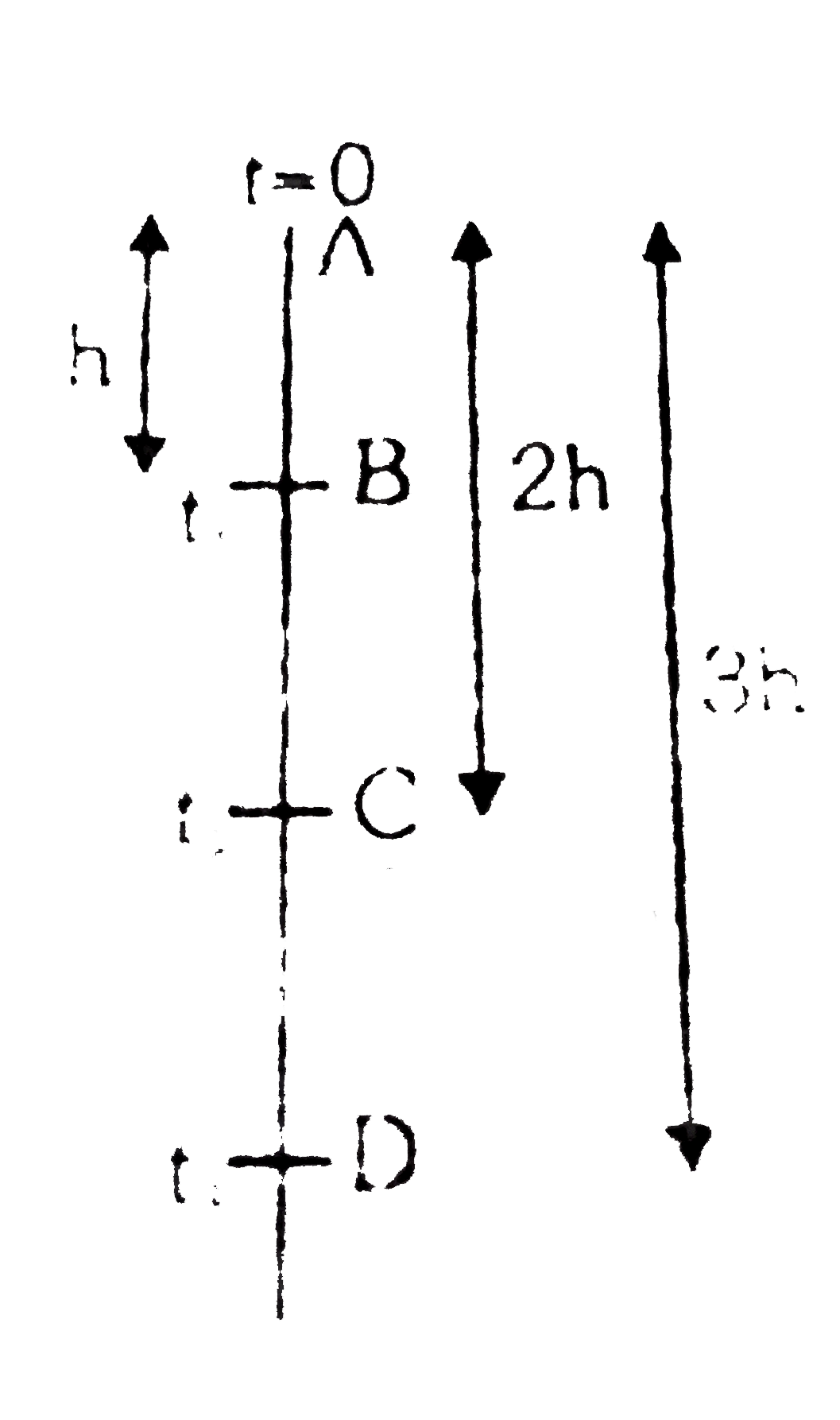
|
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-02
Explore 57 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Integer Type Question
Explore 3 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
Knowledge Check
If A, B, C and D are four numbers such that A:B=2:3,B:C=4:5,C:D=5:8, then A:D is equal to
A1:3B3:1C2:3D3:2If AB =112cm, BC=16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
A90∘B120∘C60∘D150∘Let D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
AAC⊥ABB∠BDC=90∘C∠BDC is acuteD∠BNDC>90∘
In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
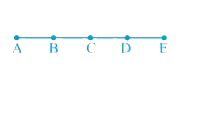
AE = ________ × AB.
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
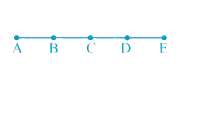
AD = AB + ________
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
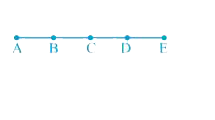
AD = AC + ___________
View SolutionLet D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
View SolutionAb Bc Cd De Ef Fg G?
View Solution