The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
![The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2). [g=10 m//s^(2)] Time of flight of the projectile is :-](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C02_E01_149_Q01.png)
Time of flight of the projectile is :-
√310s
√103s
1s
2s
The correct Answer is:A
Time of fight =2usinθg=2×√10×√3210=√310
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#43videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#56videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#25videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
The equation of trajectory of a projectile thrown from a point on the ground is y=(x−x240)m. If g=10ms−2 The maximum height reached is
View SolutionThe path followed by a body projected along y axis is given by y=√3x−(1/2)x2 . If g=10ms2, then the initial velocity of projectile will be – (x and y are in m)
View Solution
Knowledge Check
- Question 1 - Select One
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
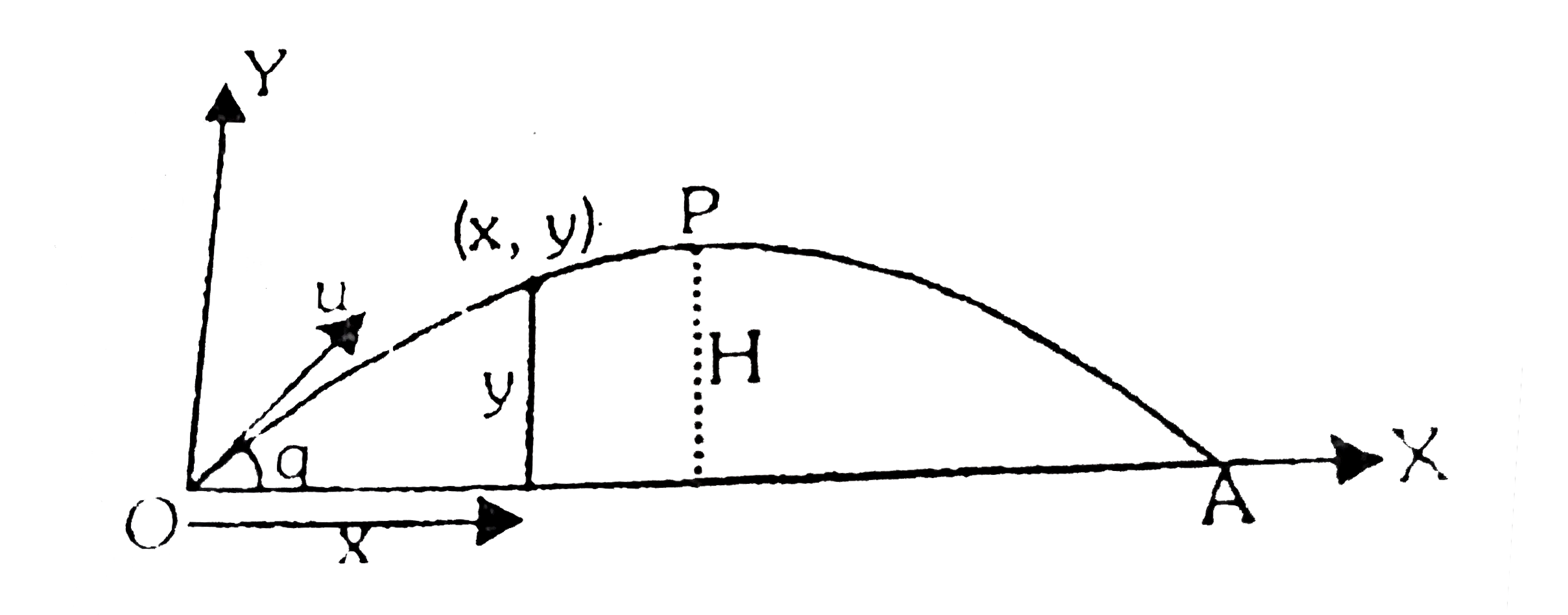
Range OA is :-A√32B√34C√3D38 - Question 2 - Select One
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-A83B38C√3D2√3 - Question 3 - Select One
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-A30∘B60∘C45∘D√3 rad
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Radius of curvature of the path of the projectile at the topmost point P is :-View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where a and b are constants and x and y are respectively horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projection form the horizontal are:
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionThe height y and distance x along the horizontal plane of a projectile on a certain planet are given by x=6tm and y=(8t2−5t2)m. The velocity with which the projectile is projected is
View SolutionFor ground to ground projectile motion equation of path is y=12x−3/4x2. Given that g=10ms−2. What is the range of the projectile ?
View Solution

