The equation of trajectory of a projectile thrown from a point on the ground is y=(x−x240)m. If g=10ms−2 The maximum height reached is
Step by step video & image solution for The equation of trajectory of a projectile thrown from a point on the ground is y=(x-x^(2)/40)m. If g=10ms^(-2) The maximum height reached is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The equation of trajectory of a projectile thrown from a level ground near the surface of earth is given by y = ax −bx2 , with y axis in vertical direction and x-axis in horizontal direction .a and b are constants. Then
AThe range of the projectile is abBAt x=a2b , the velocity of projectile becomes zeroCThe maximum height attained by projectile is a24bDThe angle of projection is tan−1(a)The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-A83B38C√3D2√3The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
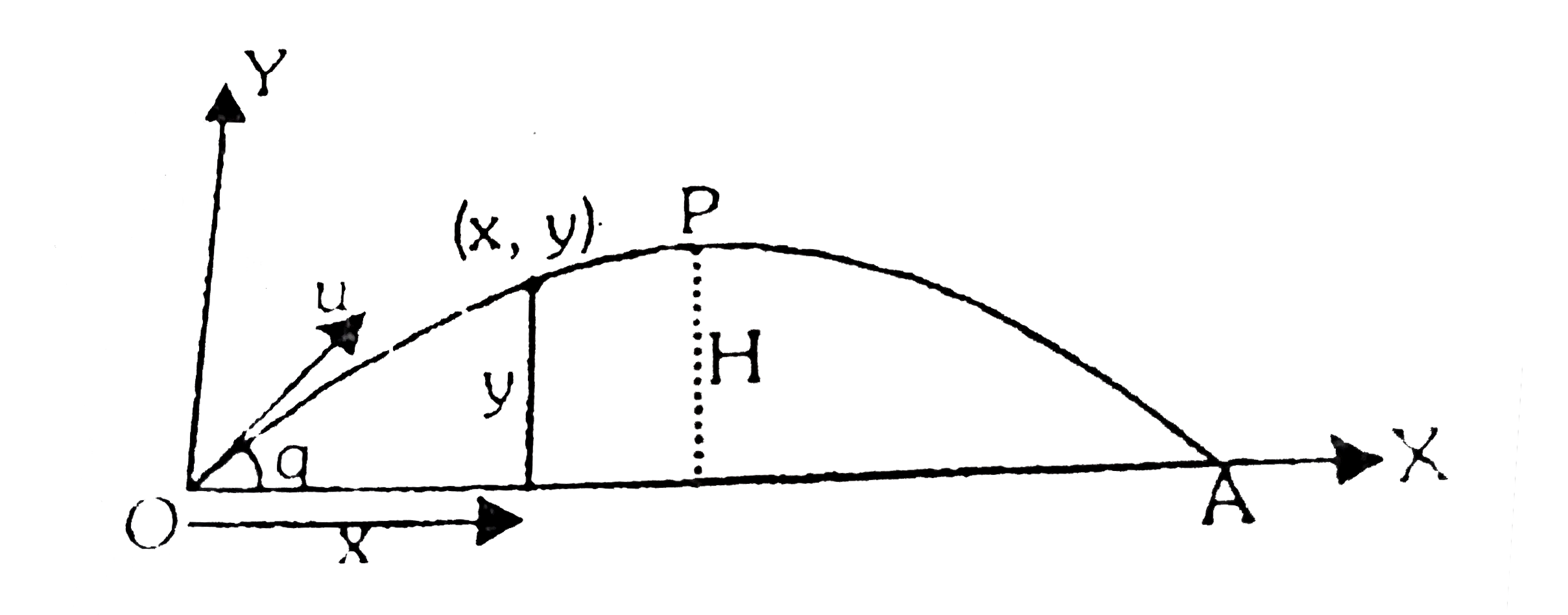
Range OA is :-A√32B√34C√3D38
The equation of a trajectory of a projectile is y=8x-4x^(2) The maximum height of the projectile is (A) 8m (B) 6m (C) 2m (D) 4m
View SolutionThe equation of the path of the projectiles is y=0.5x−0.04x2 .The initial speed of the projectile is? (g=10ms−2)
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-
View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View Solution
