Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not parallel to CD . Draw the perpendicular bisector of AB and CD. At what point do they intersect?
Step-by-Step Solution
Step 1: Draw a Circle
- Start by drawing a circle with center at point O.
- Use a compass to draw the circle. Choose a suitable radius and ensure the center is marked clearly as point O.
Step 2: Draw Two Chords
- Draw the first chord AB inside the circle. Make sure it is a straight line connecting two points on the circumference of the circle.
- Next, draw the second chord CD, ensuring that it is not parallel to chord AB. This means the angle between the two chords should not be 0 degrees.
Step 3: Draw the Perpendicular Bisector of Chord AB
- To find the perpendicular bisector of chord AB, take a compass and set it to a width greater than half the length of AB.
- With the compass point on point A, draw an arc above and below the line segment AB.
- Without changing the compass width, place the compass point on point B and draw another arc above and below the line segment AB.
- Label the intersection points of the arcs as points P and Q.
- Draw a straight line through points P and Q. This line is the perpendicular bisector of chord AB.
Step 4: Draw the Perpendicular Bisector of Chord CD
- Repeat the same process for chord CD. Set the compass to a width greater than half the length of CD.
- With the compass point on point C, draw an arc above and below the line segment CD.
- Without changing the compass width, place the compass point on point D and draw another arc above and below the line segment CD.
- Label the intersection points of these arcs as points R and S.
- Draw a straight line through points R and S. This line is the perpendicular bisector of chord CD.
Step 5: Find the Intersection Point
- The two lines you have drawn (the perpendicular bisectors of chords AB and CD) will intersect at a point. Label this intersection point as point X.
- According to the properties of circles, this point X will be the center of the circle, which is point O.
- Start by drawing a circle with center at point O.
- Use a compass to draw the circle. Choose a suitable radius and ensure the center is marked clearly as point O.
- Draw the first chord AB inside the circle. Make sure it is a straight line connecting two points on the circumference of the circle.
- Next, draw the second chord CD, ensuring that it is not parallel to chord AB. This means the angle between the two chords should not be 0 degrees.
- To find the perpendicular bisector of chord AB, take a compass and set it to a width greater than half the length of AB.
- With the compass point on point A, draw an arc above and below the line segment AB.
- Without changing the compass width, place the compass point on point B and draw another arc above and below the line segment AB.
- Label the intersection points of the arcs as points P and Q.
- Draw a straight line through points P and Q. This line is the perpendicular bisector of chord AB.
- Repeat the same process for chord CD. Set the compass to a width greater than half the length of CD.
- With the compass point on point C, draw an arc above and below the line segment CD.
- Without changing the compass width, place the compass point on point D and draw another arc above and below the line segment CD.
- Label the intersection points of these arcs as points R and S.
- Draw a straight line through points R and S. This line is the perpendicular bisector of chord CD.
- The two lines you have drawn (the perpendicular bisectors of chords AB and CD) will intersect at a point. Label this intersection point as point X.
- According to the properties of circles, this point X will be the center of the circle, which is point O.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the length of the tangent to a circle with centre O and radius 3 cm from a point P such that OP=5cm?
A7B4C8D1
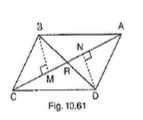
In Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
 View Solution
View SolutionDraw a circle of radius4 cm Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet ?
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View SolutionDraw a circle of radius 3 cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.
 View Solution
View Solution

