Draw an angle and label it as ∠PQR. Construct another angle ∠BAC such that ∠BAC=3 ∠PQR.
To solve the problem of constructing an angle ∠BAC such that ∠BAC=3×∠PQR, we will follow these steps:
Step 1: Draw Angle PQR
1. Use a ruler to draw a straight line. This will be one side of the angle.
2. Choose a point on this line, label it as Q.
3. Use a protractor to measure an angle. Let's say we measure 34∘ (you can choose any angle).
4. Mark the angle from point Q and label the other point as P.
5. Draw the second line from point Q through point P to complete the angle ∠PQR.
Step 2: Calculate the Measure of Angle BAC
1. Since ∠BAC=3×∠PQR, we need to calculate 3×34∘.
2. Perform the multiplication: 3×34=102∘.
3. So, ∠BAC will be 102∘.
Step 3: Construct Angle BAC
1. Draw another straight line and label a point on it as A.
2. Place the protractor at point A and measure 102∘.
3. Mark the angle from point A and label the other point as C.
4. Draw the line from point A through point C to complete the angle ∠BAC.
Final Labels
- Label the angles clearly:
- ∠PQR as 34∘
- ∠BAC as 102∘
Summary
You have now constructed two angles: ∠PQR measuring 34∘ and ∠BAC measuring 102∘, where ∠BAC is three times ∠PQR.
---
1. Use a ruler to draw a straight line. This will be one side of the angle.
2. Choose a point on this line, label it as Q.
3. Use a protractor to measure an angle. Let's say we measure 34∘ (you can choose any angle).
4. Mark the angle from point Q and label the other point as P.
5. Draw the second line from point Q through point P to complete the angle ∠PQR.
1. Since ∠BAC=3×∠PQR, we need to calculate 3×34∘.
2. Perform the multiplication: 3×34=102∘.
3. So, ∠BAC will be 102∘.
1. Draw another straight line and label a point on it as A.
2. Place the protractor at point A and measure 102∘.
3. Mark the angle from point A and label the other point as C.
4. Draw the line from point A through point C to complete the angle ∠BAC.
- Label the angles clearly:
- ∠PQR as 34∘
- ∠BAC as 102∘
You have now constructed two angles: ∠PQR measuring 34∘ and ∠BAC measuring 102∘, where ∠BAC is three times ∠PQR.
Topper's Solved these Questions
Similar Questions
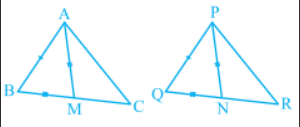
In Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
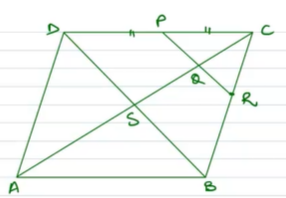
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View Solution
Knowledge Check
If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S then PQRS is a
ArectangleBparallelogramCrhombusDquardilateral whose opposite angles are supplementaryTwo circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135
In ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionPandQ are points on the ellipse x2a2+y2b2=1 whose center is C. The eccentric angles of P and Q differ by a right angle. If ∠PCQ minimum, the eccentric angle of P can be (A) π6 (B) π4 (C) π3 (D) π12
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming PQR.Figure .Show that BC=12QR
View SolutionIn a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View Solution
